题目内容
19.设x,y满足$\left\{\begin{array}{l}{x≥0}\\{x+y-2≤0}\\{ax-y-a≤0}\end{array}\right.$,若z=2x+y的最大值为$\frac{7}{2}$,则a的值为( )| A. | $-\frac{7}{2}$ | B. | 0 | C. | 1 | D. | $-\frac{7}{2}$或1 |
分析 画出约束条件的可行域,利用目标函数的最值,求出最优解,代入ax-y-a=0求解即可.
解答 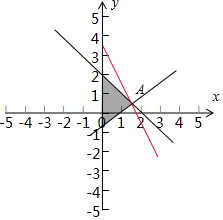 解:x,y满足$\left\{\begin{array}{l}{x≥0}\\{x+y-2≤0}\\{ax-y-a≤0}\end{array}\right.$的可行域如图:
解:x,y满足$\left\{\begin{array}{l}{x≥0}\\{x+y-2≤0}\\{ax-y-a≤0}\end{array}\right.$的可行域如图:
z=2x+y的最大值为$\frac{7}{2}$,可知直线z=2x+y经过可行域的A时,
取得最大值,
由$\left\{\begin{array}{l}{x+y-2=0}\\{2x+y=\frac{7}{2}}\end{array}\right.$解得A($\frac{3}{2}$,$\frac{1}{2}$),
A在ax-y-a=0上,可得:$\frac{3}{2}a-\frac{1}{2}-a=0$,解得a=1.
故选:C.
点评 本题考查线性规划的简单应用,目标函数的最值的求法,考查数形结合以及计算能力.

练习册系列答案
相关题目
16.在数列{an}中,a1=2,an+1=an+2,Sn为{an}的前n项和,则S10=( )
| A. | 90 | B. | 100 | C. | 110 | D. | 130 |
14.已知a、b∈R,若3-4i3=$\frac{2-bi}{a+i}$,则a+b等于( )
| A. | -9 | B. | 5 | C. | 13 | D. | 9 |
9.已知复数z满足$z=\frac{1+2i}{{{{(1-i)}^2}}}$,则在复平面内复数$\overline z$对应的点为( )
| A. | $(-1,-\frac{1}{2})$ | B. | $(1,-\frac{1}{2})$ | C. | $(-\frac{1}{2},1)$ | D. | $(-\frac{1}{2},-1)$ |