题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}4x-{x^2},x≥0\\ \frac{3}{x},x<0\end{array}$,若函数g(x)=|f(x)|-3x+b有三个零点,则实数b的取值范围为$(-∞,-6)∪(-\frac{1}{4},0]$.分析 求出函数|f(x)-3x的解析式,画出函数的图象,利用函数的极值,转化求解即可.|
解答 解:函数f(x)=$\left\{\begin{array}{l}4x-{x^2},x≥0\\ \frac{3}{x},x<0\end{array}$,若函数g(x)=|f(x)|-3x+b有三个零点,
就是h(x)=|f(x)|-3x与y=-b有3个交点,
h(x)=$\left\{\begin{array}{l}{x-{x}^{2},0≤x≤4}\\{{x}^{2}-7x,x>4}\\{-\frac{3}{x}-3x,x<0}\end{array}\right.$,画出两个函数的图象如图:
,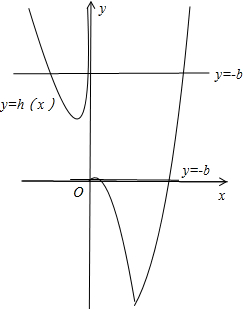
当x<0时,-$\frac{3}{x}-3x$≥6,当且仅当x=-1时取等号,此时-b>6,可得b<-6;
当0≤x≤4时,x-x2≤$\frac{1}{4}$,当x=$\frac{1}{2}$时取得最大值,满足条件的b∈(-$\frac{1}{4}$,0].
综上,b∈$(-∞,-6)∪(-\frac{1}{4},0]$.
给答案为:$(-∞,-6)∪(-\frac{1}{4},0]$.
点评 本题考查函数的零点个数的判断,考查数形结合以及计算能力.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
9.漳州水仙鳞茎硕大,箭多花繁,色美香郁,素雅娟丽,有“天下水仙数漳州”之美誉.现某水仙花雕刻师受雇每天雕刻250粒水仙花,雕刻师每雕刻一粒可赚1.2元,如果雕刻师当天超额完成任务,则超出的部分每粒多赚0.5元;如果当天未能按量完成任务,则按完成的雕刻量领取当天工资.
(Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
以10天记录的各雕刻量的频率作为各雕刻量发生的概率.
(ⅰ)在当天的收入不低于276元的条件下,求当天雕刻量不低于270个的概率;
(ⅱ)若X表示雕刻师当天的收入(单位:元),求X的分布列和数学期望.
(Ⅰ)求雕刻师当天收入(单位:元)关于雕刻量n(单位:粒,n∈N)的函数解析式f(n);
(Ⅱ)该雕刻师记录了过去10天每天的雕刻量n(单位:粒),整理得如表:
| 雕刻量n | 210 | 230 | 250 | 270 | 300 |
| 频数 | 1 | 2 | 3 | 3 | 1 |
(ⅰ)在当天的收入不低于276元的条件下,求当天雕刻量不低于270个的概率;
(ⅱ)若X表示雕刻师当天的收入(单位:元),求X的分布列和数学期望.
1.在信息时代的今天,随着手机的发展,“微信”越来越成为人们交流的一种方式,某机构对“使用微信交流”的态度进行调查,随机抽取了100人,他们年龄的频数分布及对“使用微信交流”赞成的人数如下表:(注:年龄单位:岁)
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的2×2列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
(2)若从年龄在[55,65),[65,75)的别调查的人中各随机选取两人进行追踪调查,记选中的4人中赞成“使用微信交流”的人数为X,求随机变量X的分布列及数学期望.
参考数据:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 10 | 30 | 30 | 20 | 5 | 5 |
| 赞成人数 | 8 | 25 | 24 | 10 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
参考数据:
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 6.635 | 7.879 | 10.828 |
2.对于下列说法正确的是( )
| A. | 若f(x)是奇函数,则f(x)是单调函数 | |
| B. | 命题“若x2-x-2=0,则x=1”的逆否命题是“若x≠1,则x2-x-2=0” | |
| C. | 命题p:?x∈R,2x>1024,则¬p:?x0∈R,${2^{x_0}}<1024$ | |
| D. | 命题“?x∈(-∞,0),2x<x2”是真命题 |
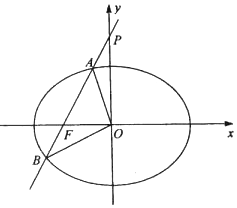 已知椭圆C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点为F(-1,0),左准线为x=-2.
已知椭圆C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左焦点为F(-1,0),左准线为x=-2.