题目内容
对于定义在区间D上的函数f(x),若任给x0∈D,均有f(x0)∈D,则称函数f(x)在区间D上封闭.
(1)试判断f(x)=2x-1在区间[0,1]上是否封闭,并说明理由;
(2)若函数g(x)=
在区间[2,9]上封闭,求实数m的取值范围;
(3)若函数h(x)=x3-3x在区间[a,b](a,b∈Z)上封闭,求a,b的值.
(1)试判断f(x)=2x-1在区间[0,1]上是否封闭,并说明理由;
(2)若函数g(x)=
| 2x+m |
| x+2 |
(3)若函数h(x)=x3-3x在区间[a,b](a,b∈Z)上封闭,求a,b的值.
考点:函数单调性的性质
专题:函数的性质及应用
分析:(1)根据f(x)在区间[0,1]上单调递增,可得函数的值域为[-1,1].由[-1,1]?[0,1],可得结论.
(2)根据函数g(x)=
在区间[2,9]上封闭,分类讨论求得实数m的取值范围.
(3)利用导数研究h(x)的单调性,分类讨论,求得m的范围.
(2)根据函数g(x)=
| 2x+m |
| x+2 |
(3)利用导数研究h(x)的单调性,分类讨论,求得m的范围.
解答:
解:(1)∵f(x)=2x-1在区间[0,1]上单调递增,所以函数的值域为[-1,1].
而[-1,1]?[0,1],所以f(x)在区间[0,1]上不是封闭的.
(2)因为函数g(x)=
在区间[2,9]上封闭,
①当m=4时,函数g(x)的值域为{2}⊆[2,9],适合题意.
②当m>4时,函数g(x)在区间[2,9]上单调递减,g(x)的值域为[
,
],
由为[
,
]⊆[2,9],得
,解得4≤m≤32.
③当m<4时,在区间[2,9]上有g(x)=
=2+
<2,显然不合题意.
综上所述,实数m的取值范围是[4,32].
(3)因为函数h(x)=x3-3x,所以h′(x)=3(x+1)(x-1),
所以h(x)在(-∞,-1)、(1,+∞)上递增,在(-1,1)上递减.
①当a<b≤-1时,h(x)在区间[a,b]上递增,所以
,
即
,显然a、b无解.
②当a≤-1且-1<b≤1时,hmin(x)=h(-1)=2>b,不合题意.
③当a≤-1且b>1时,因为h(-1)=2,h(1)=-2都在函数的值域内,
∴a≤-2,b≥2.
又
,即
,解得:
,故有a=-2,b=2.
④当-1≤a<b≤1时,h(x)在区间[a,b]上递减,则
.
∵a、b∈z,经验证,均不合题意.
⑤当-1<a≤1 且b>1时,hmin(x)=h(1)=-2<a,∴此情况不合题意.
⑥当b>a≥1时,h(x)在区间[a,b]上递增,所以
,
此时无解.
综上可得,所求的整数a、b的值为a=-2,b=2.
而[-1,1]?[0,1],所以f(x)在区间[0,1]上不是封闭的.
(2)因为函数g(x)=
| 2x+m |
| x+2 |
①当m=4时,函数g(x)的值域为{2}⊆[2,9],适合题意.
②当m>4时,函数g(x)在区间[2,9]上单调递减,g(x)的值域为[
| 18+m |
| 11 |
| 4+m |
| 4 |
由为[
| 18+m |
| 11 |
| 4+m |
| 4 |
|
③当m<4时,在区间[2,9]上有g(x)=
| 2x+m |
| x+2 |
| m-4 |
| x+2 |
综上所述,实数m的取值范围是[4,32].
(3)因为函数h(x)=x3-3x,所以h′(x)=3(x+1)(x-1),
所以h(x)在(-∞,-1)、(1,+∞)上递增,在(-1,1)上递减.
①当a<b≤-1时,h(x)在区间[a,b]上递增,所以
|
即
|
②当a≤-1且-1<b≤1时,hmin(x)=h(-1)=2>b,不合题意.
③当a≤-1且b>1时,因为h(-1)=2,h(1)=-2都在函数的值域内,
∴a≤-2,b≥2.
又
|
|
|
④当-1≤a<b≤1时,h(x)在区间[a,b]上递减,则
|
∵a、b∈z,经验证,均不合题意.
⑤当-1<a≤1 且b>1时,hmin(x)=h(1)=-2<a,∴此情况不合题意.
⑥当b>a≥1时,h(x)在区间[a,b]上递增,所以
|
此时无解.
综上可得,所求的整数a、b的值为a=-2,b=2.
点评:本题主要考查函数的单调性的应用,新定义,其中,分类讨论,是解题的关键和难点,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 在一项农业试验中,为了比较两种肥料对于某种果树的施肥效果,随机选取了施用这两种肥料的果树各10棵的产量(单位:kg):
在一项农业试验中,为了比较两种肥料对于某种果树的施肥效果,随机选取了施用这两种肥料的果树各10棵的产量(单位:kg):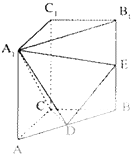 直三棱柱ABC-A1B1C1中,AC=CB=AA1=2,∠ACB=90°,E是BB1的中点,D∈AB,∠A1DE=90°.
直三棱柱ABC-A1B1C1中,AC=CB=AA1=2,∠ACB=90°,E是BB1的中点,D∈AB,∠A1DE=90°. 
 如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.
如图,四棱锥P-ABCD中,PB⊥底面ABCD,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA.