题目内容
已知椭圆C的长轴长为2
,一个焦点的坐标为(1,0).直线l:y=kx与椭圆C交于A,B两点,点P为椭圆上不同于A,B的任意一点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设l的斜率k=1,P为椭圆的右顶点.求△ABP的面积.
(Ⅲ)若直线AP,BP的斜率存在且分别为k1,k2.求k1k2.
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设l的斜率k=1,P为椭圆的右顶点.求△ABP的面积.
(Ⅲ)若直线AP,BP的斜率存在且分别为k1,k2.求k1k2.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)由椭圆的定义容易求得a,c,然后结合a2=b2+c2求出b,焦点在x轴上,所以方程可求;
(Ⅱ)S△ABP=S△OAP+S△OBP=
OB•|yA|+
OB|yB|=
a|yA-yB|,然后将直线方程代入椭圆方程,消去x,得到关于y的一元二次方程,其两个根就是yA,yB,容易求得|yA-yB|,则面积可求;
(Ⅲ)将已知与所求坐标化,然后化简.注意到椭圆的对称性、直线y=kx过原点和椭圆相交,则A,B两点横纵坐标分别互为相反数,同时将P点坐标给出来,再将k1,k2用A,B,P坐标表示,然后将k1k2表示出来进行化简即可,注意消元.
(Ⅱ)S△ABP=S△OAP+S△OBP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅲ)将已知与所求坐标化,然后化简.注意到椭圆的对称性、直线y=kx过原点和椭圆相交,则A,B两点横纵坐标分别互为相反数,同时将P点坐标给出来,再将k1,k2用A,B,P坐标表示,然后将k1k2表示出来进行化简即可,注意消元.
解答:
解:(Ⅰ)长轴长为2
,一个焦点的坐标为(1,0),
∴a=
,c=1,且焦点在x轴上,
∴b2=a2-c2=1,
∴椭圆方程为
+y2=1.
(Ⅱ)由已知直线l方程为y=x,
代入
+y2=1后化简得
y=
或-
,
∴S△ABP=S△OAP+S△OBP=
OB•|yA|+
OB|yB|=
a|yA-yB|
=
×
×
=
;
(Ⅲ)由椭圆的对称性且y=kx过原点,不妨设A(x,y),B(-x,-y),P(m,n),
∴k1k2=
•
=
①,
又
+y2=1,
+n2=1,
∴①=
=
=-
.
∴k1k2=-
.
| 2 |
∴a=
| 2 |
∴b2=a2-c2=1,
∴椭圆方程为
| x2 |
| 2 |
(Ⅱ)由已知直线l方程为y=x,
代入
| x2 |
| 2 |
y=
| ||
| 3 |
| ||
| 3 |
∴S△ABP=S△OAP+S△OBP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
(Ⅲ)由椭圆的对称性且y=kx过原点,不妨设A(x,y),B(-x,-y),P(m,n),
∴k1k2=
| n-y |
| m-x |
| n+y |
| m+x |
| n2-y2 |
| m2-x2 |
又
| x2 |
| 2 |
| m2 |
| 2 |
∴①=
(1-
| ||||
| m2-x2 |
-
| ||
| m2-x2 |
| 1 |
| 2 |
∴k1k2=-
| 1 |
| 2 |
点评:第(1)(2)问属常规题型,较为简单;第三问先把k1,k2坐标化,充分注意到A,B两点的对称性消元,再利用椭圆方程消元,最后将k1k2化简求值.

练习册系列答案
相关题目
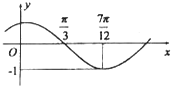 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<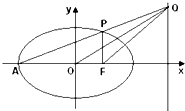 如图,在平面直角坐标系xOy中,已知A,F分别为椭圆C:
如图,在平面直角坐标系xOy中,已知A,F分别为椭圆C: