题目内容
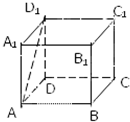
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点D到平面ACD1的距离 .

考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:先求得VD1-ADC,进而求得AD1,AC,CD1,进而求得△ACD1的面积,最后利用等体积法求得答案.
解答:
解:依题意知DD1⊥平面ADC,
则VD1-ADC=
•DD1•S△ADC=
×1×
×1×1=
,
AD1=
=
,AC=
=
,CD1=
=
,
∴AD1=AC=CD1,
∴S△ACD1=
×
×
=
,
设D到平面ACD1的距离为d,
则VD-ACD1=
•d•S△ACD1=
•d•
=VD1-ADC=
,
∴d=
.
故答案为:
.
则VD1-ADC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
AD1=
| 1+1 |
| 2 |
| 1+1 |
| 2 |
| 1+1 |
| 2 |
∴AD1=AC=CD1,
∴S△ACD1=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
设D到平面ACD1的距离为d,
则VD-ACD1=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 6 |
∴d=
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题主要考查了点面的距离的计算.常采用等体积法来解决.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
下列向量中不是单位向量的是( )
| A、(-1,0) | ||||||||
| B、(1,1) | ||||||||
| C、(cosa,sina) | ||||||||
D、
|

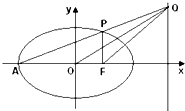 如图,在平面直角坐标系xOy中,已知A,F分别为椭圆C:
如图,在平面直角坐标系xOy中,已知A,F分别为椭圆C: