题目内容
已知曲线C的极坐标方程式ρ2=2ρsinθ+3,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是
(t为参数,m为常熟)
(1)写出曲线C的参数方程,直线l的普通方程
(2)当曲线C与直线l有公共点时,求m的取值范围.
|
(1)写出曲线C的参数方程,直线l的普通方程
(2)当曲线C与直线l有公共点时,求m的取值范围.
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)曲线C的极坐标方程式ρ2=2ρsinθ+3,把
代入即可得出;进而可得曲线C的参数方程为
.由直线l的参数方程
(t为参数),消去参数t可得3x-4y-3m=0.
(2)曲线C与直线l有公共点,可得圆心到直线的距离≤r,解出即可.
|
|
|
(2)曲线C与直线l有公共点,可得圆心到直线的距离≤r,解出即可.
解答:
解:(1)曲线C的极坐标方程式ρ2=2ρsinθ+3,化为x2+y2=2y+3,配方为x2+(y-1)2=4.
可得曲线C的参数方程为
.
由直线l的参数方程
(t为参数),消去参数t可得3x-4y-3m=0.
(2)∵曲线C与直线l有公共点,∴
≤2,
化为|3m+4|≤10,∴-10≤3m+4≤10,解得-
≤m≤2.
∴m的取值范围是[-
,2].
可得曲线C的参数方程为
|
由直线l的参数方程
|
(2)∵曲线C与直线l有公共点,∴
| |0-4-3m| | ||
|
化为|3m+4|≤10,∴-10≤3m+4≤10,解得-
| 14 |
| 3 |
∴m的取值范围是[-
| 14 |
| 3 |
点评:本题考查了圆的极坐标方程化为直角坐标方程及参数方程、点到直线的距离公式、直线与圆的位置关系,考查了计算能力,属于基础题.

练习册系列答案
相关题目
对于定义域为R的函数f(x),若f(x)在(-∞,0)和(0,+∞)上均有零点,则称函数f(x)为“含界点函数”,则下列四个函数中,不是“含界点函数”的是( )
| A、f(x)=x2+bx-1(b∈R) |
| B、f(x)=2-|x-1| |
| C、f(x)=2x-x2 |
| D、f(x)=x-sinx |
设0<a≤1,函数f(x)=x+
,g(x)=x-lnx,若对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立,则a的取值范围为( )
| a |
| x |
| A、(0,1] | ||
| B、(0,e-2] | ||
| C、[e-2,1] | ||
D、[1-
|
已知长方体ABCD-A1B1C1D1,下列向量的数量积一定不为0的是( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
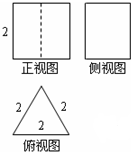 已知一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在一个球面上,则球的表面积是( )
已知一个空间几何体的三视图如图所示,且这个空间几何体的所有顶点都在一个球面上,则球的表面积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
一个几何体得三视图如图所示,则该几何体的体积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、5
|
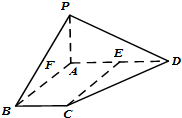 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,E为AD的中点,∠BAD=120°,PA=AB=BC=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,E为AD的中点,∠BAD=120°,PA=AB=BC=