题目内容
计算定积分:
(1)∫01e2xdx;
(2)
cos2xdx.
(1)∫01e2xdx;
(2)
| ∫ |
-
|
考点:定积分
专题:导数的综合应用
分析:找出被积函数的原函数,代入积分上限和下限求值.
解答:
解:(1)∫01e2xdx=(
e2x)
=
e2-
;
(2)
cos2xdx=(
sin2x)
=sin
.
| 1 |
| 2 |
| | | 1 0 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)
| ∫ |
-
|
| 1 |
| 2 |
| | |
-
|
| 1 |
| 3 |
点评:本题考查了定积分的计算;关键是正确找出被积函数的原函数.

练习册系列答案
相关题目
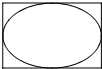 如图所示,矩形长为3,宽为2,在矩形内随机撒200颗黄豆,数得落在椭圆内的黄豆数为160颗,依据此实验数据可以估计出椭圆的面积约为( )
如图所示,矩形长为3,宽为2,在矩形内随机撒200颗黄豆,数得落在椭圆内的黄豆数为160颗,依据此实验数据可以估计出椭圆的面积约为( )| A、4.7 | B、4.8 |
| C、1.2 | D、1.3 |
若双曲线
+
=1的离心率为
,则实数k的值为( )
| x2 |
| 3 |
| y2 |
| k |
| 3 |
A、-
| ||
B、
| ||
| C、-6 | ||
| D、6 |
