题目内容
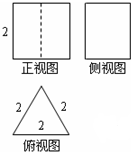已知一个空间几何体的三视图如图所示，且这个空间几何体的所有顶点都在一个球面上，则球的表面积是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图知，几何体是一个三棱柱，三棱柱的底面是边长为2的正三角形，侧棱长是2，根据三棱柱的两个底面的中心的中点与三棱柱的顶点的连线就是外接球的半径，求出半径即可求出球的表面积．
解答：
解：由三视图知，几何体是一个三棱柱，三棱柱的底面是边长为2的正三角形，侧棱长是2，
三棱柱的两个底面的中心的中点与三棱柱的顶点的连线就是外接球的半径，
r=
=
，球的表面积4πr2=4π×
=
π．
故选：A．
三棱柱的两个底面的中心的中点与三棱柱的顶点的连线就是外接球的半径，
r=
(
|
|
| 7 |
| 3 |
| 28 |
| 3 |
故选：A．
点评：本题考查了由三视图求三棱柱的外接球的表面积，利用棱柱的几何特征求外接球的半径是解题的关键．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
已知f（x）=ln（x+1）-ln（1-x），x∈（-1，1），现有下列命题：
①f（-x）=-f（x）；②f(
)=2f(x)；③f（x）在（-1，1）上是增函数，
其中正确命题的序号是（ ）
①f（-x）=-f（x）；②f(
| 2x |
| 1+x2 |
其中正确命题的序号是（ ）
| A、①②③ | B、②③ | C、①③ | D、①② |
下列图形中不可能是三棱柱在平面上的投影的是（ ）
A、 |
B、 |
C、 |
D、 |
某几何体的三视图如图，则该几何体的表面积为（ ）
A、3+
| ||
| B、6 | ||
C、3+
| ||
D、2+
|
已知向量
与
的夹角为30°，且|
|=1，|2
-
|=1，则|
|=（ ）
| a |
| b |
| a |
| a |
| b |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
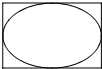如图所示，矩形长为3，宽为2，在矩形内随机撒200颗黄豆，数得落在椭圆内的黄豆数为160颗，依据此实验数据可以估计出椭圆的面积约为（ ）| A、4.7 | B、4.8 |
| C、1.2 | D、1.3 |