题目内容

点M与定点F（2，0）的距离和它到直线x=8的距离的比是1：2，求点Md轨迹方程，并说明轨迹是什么图形．
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：设M（x，y）是轨迹上任意一点，依题意
(x-2)2+y2
|x-8|
=
1
2
，由此能求出点M的轨迹方程与点M的轨迹．
解答： 解：（1）设M（x，y）是轨迹上任意一点，
依题意，
(x-2)2+y2
|x-8|
=
1
2
，
即2
(x-2)2+y2
=|x-8|
两边平方得，4（x-2）2+y2=（x-8）2，
化简得点M的轨迹方程为
x2
16
+
y2
12
=1，
∴点M的轨迹方程为
x2
16
+
y2
12
=1，点M的轨迹是椭圆．
点评：本题考查点的轨迹方程的求法，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
若不等于1的三个正数a、b、c成等比数列，则（2-logba）（1+logca）=
 
．
设数列{an}中，首项a1=1，点（an，an+1）（n=1，2，3，…）均在直线y=2x+1上
（1）求a2，a3，a4的值；
（2）求数列{an}的通项公式．
已知函数f（x）=
1，x是有理数
0，x是无理数
，下列命题是真命题的是
 
（只填命题序号）．
①函数f（x）是偶函数；②对任意x∈R，f（x+
2
）=f（x）；
③对任意x∈R，f（x+2）=f（x）；
④对任意x，y∈R，f（x+y）=
1
2
（f（x）+f（x））；
⑤若存在x，y∈R，使得f（x+y）=f（x）+f（y），则x，y都为无理数．
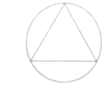某人随机地向如图所示的正三角形及其外接圆区域内部设计（不包括三角形及其外接圆的边界），则针孔到正三角形内部（不包括边界）的概率为（　　）
A、
3
3
2π
B、
3
π
C、
3
3
4π
D、
3
3
5π
设函数f（x）=
a
x2
+lnx，g（x）=x3-x2-3．
（Ⅰ）讨论函数f（x）的单调性；
（Ⅱ）若存在x1，x2∈[-
1
3
，3]，使得g（x1）-g（x2）≥M成立，求满足条件的最大整数M；
（Ⅲ）如果对任意的s，t∈[
1
3
，2]，都有sf（s）≥g（t）成立，求实数a的取值范围．
已知函数f（x）=x2+2ax+1-a在（-1，1）上有零点，求a的取值范围．
已知函数f（x）=2x+k•2-x，k∈R．
（1）若函数f（x）为奇函数，求实数k的值；
（2）若对任意的x∈[0，+∞）都有f（x）＜0成立，求实数k的取值范围．
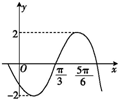已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-π＜φ＜0）的部分图象如图，则f（x）的表达式为（　　）
A、f（x）=2sin（
1
2
x-
2
3
π）
B、f（x）=2sin（x-
2
3
π）
C、f（x）=2sin（
1
2
x+
π
3
）
D、f（x）=2sin（2x-
2
3
π）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网