题目内容
已知函数f(x)=x2+2ax+1-a在(-1,1)上有零点,求a的取值范围.
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:分对称轴的位置进行讨论,从而确定函数的零点的位置,从而解得.
解答:
解:当-a≤-1,即a≥1时,
f(-1)•f(1)<0;
故(1-2a+1-a)(1+2a+1-a)<0;
解得,a≥1;
当-a≥1,即a≤-1时,
f(-1)•f(1)<0,
即(1-2a+1-a)(1+2a+1-a)<0,
解得,a<-2;
当-1<-a<1,即-1<a<1时,
△=4a2-4(1-a)≥0;
解得,a≥
;
此时,f(1)=a+2>0;
故
≤a<1;
综上所述,a的取值范围为a≥
或a<-2.
f(-1)•f(1)<0;
故(1-2a+1-a)(1+2a+1-a)<0;
解得,a≥1;
当-a≥1,即a≤-1时,
f(-1)•f(1)<0,
即(1-2a+1-a)(1+2a+1-a)<0,
解得,a<-2;
当-1<-a<1,即-1<a<1时,
△=4a2-4(1-a)≥0;
解得,a≥
| ||
| 2 |
此时,f(1)=a+2>0;
故
| ||
| 2 |
综上所述,a的取值范围为a≥
| ||
| 2 |
点评:本题考查了二次函数的零点的位置,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知△ABC三个顶点的坐标分别为A(0,0),B(2,2),C(0,c),若
⊥
,那么c的值是( )
| AB |
| BC |
| A、-1 | B、3 | C、-3 | D、4 |
已知函数f(x)=
-(x-1)2+
,则函数f(x)的所有零点的和是( )
| 3 |
| |x-1|-2 |
| 3 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
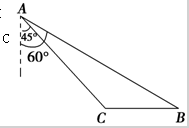 如图,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(
如图,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?( 