题目内容
20.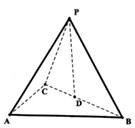 如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.
如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.(Ⅰ)求证:平面ABC⊥平面PBC;
(Ⅱ)若点M是线段AP上一动点,点N为线段AB的四等分点(靠近B点),求直线NM与平面PAD所成角的余弦值的最小值.
分析 (Ⅰ)取AB中点E,连接DE,PE,可得DE∥AC,结合已知得DE⊥AB,求解三角形证得AD⊥PD,利用线面垂直的判定可得AD⊥平面PBC,从而得到平面ABC⊥平面PBC;
(Ⅱ)由(Ⅰ)知PD⊥CB,以D为坐标原点,分别以DA、DB、DP所在直线为x、y、z轴建立空间直角坐标系,设$\overrightarrow{AM}=λ\overrightarrow{AP}$(0≤λ≤1),把M的坐标用含有λ的代数式表示,求得$\overrightarrow{MN}$的坐标.平面PAD的一个法向量$\overrightarrow{m}=(0,1,0)$,可得直线NM与平面PAD所成角的正弦值,利用二次函数求得直线NM与平面PAD所成角的正弦的最大值,即余弦值最小值.
解答 (Ⅰ)证明:如图,取AB中点E,连接DE,PE,则DE∥AC,
∵AC⊥AB,∴DE⊥AB,
∵PAB为正三角形,∴PE⊥AB,则∠PED为二面角P-AB-D的平面角,cos∠PED=$\frac{\sqrt{3}}{3}$.
∵DE=$\frac{1}{2}AC=2$,PE=$2\sqrt{3}$,由余弦定理可得PD2=PE2+DE2-2×PE×DE=12+4-2×$2\sqrt{3}×2×\frac{\sqrt{3}}{3}$=8.
在等腰直角三角形ABC中,可得AD=$2\sqrt{2}$,满足PD2+AD2=8+8=16=PA2,
∴AD⊥PD,又AD⊥BC且PD∩BC=D,
∴AD⊥平面PBC,又AD?平面ABC,则平面ABC⊥平面PBC;
(Ⅱ)解:由(Ⅰ)知PD2+DB2=PB2,则PD⊥CB,
以D为坐标原点,分别以DA、DB、DP所在直线为x、y、z轴建立空间直角坐标系,
则N($\frac{\sqrt{2}}{2},\frac{3\sqrt{2}}{2},0$),A($2\sqrt{2}$,0,0),P(0,0,$2\sqrt{2}$),
设M(x,0,z),且$\overrightarrow{AM}=λ\overrightarrow{AP}$(0≤λ≤1),则($x-2\sqrt{2}$,0,z)=($-2\sqrt{2}λ$,0,$2\sqrt{2}λ$),
∴x=$2\sqrt{2}+2\sqrt{2}λ$,z=$2\sqrt{2}λ$,则M($2\sqrt{2}+2\sqrt{2}λ$,0,$2\sqrt{2}λ$).
∴$\overrightarrow{MN}=(-\frac{3\sqrt{2}}{2}-2\sqrt{2}λ,\frac{3\sqrt{2}}{2},-2\sqrt{2}λ)$.
平面PAD的一个法向量$\overrightarrow{m}=(0,1,0)$,
∴直线NM与平面PAD所成角的正弦值为|cos<$\overrightarrow{m},\overrightarrow{MN}$>
|=|$\frac{\frac{3\sqrt{2}}{2}}{\sqrt{(-\frac{3\sqrt{2}}{2}-2\sqrt{2}λ)^{2}+(\frac{3\sqrt{2}}{2})^{2}+(-2\sqrt{2}λ)^{2}}×1}$|
=$\frac{\frac{3\sqrt{2}}{2}}{\sqrt{16{λ}^{2}+12λ+9}}$.
∴当λ=0时,直线NM与平面PAD所成角的正弦值最大,即余弦值最小为$\frac{\sqrt{2}}{2}$.
点评 本题考查面面垂直的判定,考查空间想象能力和思维能力,训练了利用空间向量求解线面角,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | (1,2) | B. | (1,4) | C. | (2,4) | D. | (4,16) |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 身高x(厘米) | 192 | 164 | 172 | 177 | 176 | 159 | 171 | 166 | 182 | 166 |
| 脚长y(码) | 48 | 38 | 40 | 43 | 44 | 37 | 40 | 39 | 46 | 39 |
| 序号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 身高x(厘米) | 169 | 178 | 167 | 174 | 168 | 179 | 165 | 170 | 162 | 170 |
| 脚长y(码) | 43 | 41 | 40 | 43 | 40 | 44 | 38 | 42 | 39 | 41 |
(Ⅱ)若“身高大于175厘米”为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”为“大码”,“脚长小于等于42码”的为“非大码”.请根据上表数据完成2×2列联表:并根据列联表中数据说明能有多大的可靠性认为脚的大小与身高之间有关系?
(Ⅲ)若按下面的方法从这20人中抽取1人来核查测量数据的误差:将一个标有1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号,求:抽到“无效序号(超过20号)”的概率.
附表及公式:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
$b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}},a=\overline y-b\overline x$.
 如图,梯形ABCD,|$\overrightarrow{DA}$|=2,∠CDA=$\frac{π}{3}$,$\overrightarrow{DA}$=2$\overrightarrow{CB}$,E为AB中点,$\overrightarrow{DP}$=λ$\overrightarrow{DC}$(0≤λ≤1).
如图,梯形ABCD,|$\overrightarrow{DA}$|=2,∠CDA=$\frac{π}{3}$,$\overrightarrow{DA}$=2$\overrightarrow{CB}$,E为AB中点,$\overrightarrow{DP}$=λ$\overrightarrow{DC}$(0≤λ≤1).