题目内容
15.已知向量$\overrightarrow a=({1,3}),\overrightarrow b=({m,2}),\overrightarrow c=({3,4})$,且$({\overrightarrow a-3\overrightarrow b})⊥\overrightarrow c$(1)求实数m的值;
(2)求向量$\overrightarrow a,\overrightarrow b$的夹角θ.
分析 (1)根据向量坐标公式先求出向量坐标,根据向量数量积的坐标公式进行求解即可.
(2)根据向量数量积的应用求出向量长度,进行求解即可.
解答 解:(1)∵$\overrightarrow a=({1,3}),\overrightarrow b=({m,2}),\overrightarrow c=({3,4})$,
∴$\overrightarrow{a}$-3$\overrightarrow{b}$=(1.3)-(3m,6)=(1-3m,-3),
∵$({\overrightarrow a-3\overrightarrow b})⊥\overrightarrow c$,
∴($\overrightarrow{a}$-3$\overrightarrow{b}$)•$\overrightarrow{c}$=3(1-3m)+(-3)×4=-9m-9=0,
得m=-1.
(2)由(1)知,$\overrightarrow{a}$=(1,3),$\overrightarrow{b}$=(-1,2),
则$\overrightarrow{a}$•$\overrightarrow{b}$=5,|$\overrightarrow{a}$|=$\sqrt{10}$,|$\overrightarrow{b}$|=$\sqrt{5}$,
则cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{5}{\sqrt{10}×\sqrt{5}}$=$\frac{\sqrt{2}}{2}$,
∵θ∈(0,π),
∴θ=$\frac{π}{4}$.
点评 本题主要考查向量数量积的应用,根据向量垂直与向量数量积的关系以及向量夹角与向量数量积的关系是解决本题的关键.

| A. | 3 | B. | 1 | C. | 0 | D. | 2 |
| A. | 0.2 | B. | 0.6 | C. | 0.4 | D. | 0.3 |
| A. | $[\frac{2}{3},1)$ | B. | $[\frac{1}{3},1)$ | C. | $[\frac{1}{3},1)∪(1,3]$ | D. | (1,3] |
| A. | ±1 | B. | ±2 | C. | $±\sqrt{2}$ | D. | $±\sqrt{3}$ |
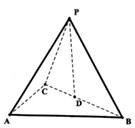 如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.
如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.