题目内容
5. 如图,梯形ABCD,|$\overrightarrow{DA}$|=2,∠CDA=$\frac{π}{3}$,$\overrightarrow{DA}$=2$\overrightarrow{CB}$,E为AB中点,$\overrightarrow{DP}$=λ$\overrightarrow{DC}$(0≤λ≤1).
如图,梯形ABCD,|$\overrightarrow{DA}$|=2,∠CDA=$\frac{π}{3}$,$\overrightarrow{DA}$=2$\overrightarrow{CB}$,E为AB中点,$\overrightarrow{DP}$=λ$\overrightarrow{DC}$(0≤λ≤1).(Ⅰ)当λ=$\frac{1}{3}$,用向量$\overrightarrow{DA}$,$\overrightarrow{DC}$表示的向量$\overrightarrow{PE}$;
(Ⅱ)若|$\overrightarrow{DC}$|=t(t为大于零的常数),求|$\overrightarrow{PE}$|的最小值并指出相应的实数λ的值.
分析 (I)过C作CF∥AB,交AD于F,则F为AD中点,用$\overrightarrow{DA},\overrightarrow{DC}$表示出$\overrightarrow{PC},\overrightarrow{CB},\overrightarrow{BE}$,利用三角形法则即可得出结论;
(II)根据(I)得出$\overrightarrow{PE}$的表达式,两边平方得出${\overrightarrow{PE}}^{2}$关于λ的二次函数,根据二次函数的性质求出最值.
解答  解:(I)过C作CF∥AB,交AD于F,
解:(I)过C作CF∥AB,交AD于F,
则四边形ABCF是平行四边形,F是AD的中点,
∴$\overrightarrow{BE}$=$\frac{1}{2}$$\overrightarrow{BA}$=$\frac{1}{2}$$\overrightarrow{CF}$=$\frac{1}{2}$$\overrightarrow{DF}$-$\frac{1}{2}$$\overrightarrow{DC}$=$\frac{1}{4}$$\overrightarrow{DA}$-$\frac{1}{2}$$\overrightarrow{DC}$,
λ=$\frac{1}{3}$时,$\overrightarrow{PC}=\frac{2}{3}\overrightarrow{DC}$,
∴$\overrightarrow{PE}$=$\overrightarrow{PC}+\overrightarrow{CB}+\overrightarrow{BE}$=$\frac{2}{3}$$\overrightarrow{DC}$+$\frac{1}{2}$$\overrightarrow{DA}$+$\frac{1}{4}$$\overrightarrow{DA}$-$\frac{1}{2}$$\overrightarrow{DC}$=$\frac{3}{4}$$\overrightarrow{DA}$+$\frac{1}{6}$$\overrightarrow{DC}$.
(II)∵$\overrightarrow{DP}$=λ$\overrightarrow{DC}$,∴$\overrightarrow{PC}$=(1-λ)$\overrightarrow{DC}$,
∴$\overrightarrow{PE}$=$\overrightarrow{PC}+\overrightarrow{CB}+\overrightarrow{BE}$=(1-λ)$\overrightarrow{DC}$+$\frac{1}{2}$$\overrightarrow{DA}$+$\frac{1}{4}$$\overrightarrow{DA}$-$\frac{1}{2}$$\overrightarrow{DC}$=($\frac{1}{2}-λ$)$\overrightarrow{DC}$+$\frac{3}{4}$$\overrightarrow{DA}$,
∵$\overrightarrow{DC}•\overrightarrow{DA}$=2tcos60°=t,${\overrightarrow{DC}}^{2}$=t2,${\overrightarrow{DA}}^{2}$=4,
∴$\overrightarrow{PE}$2=($\frac{1}{2}-λ$)2t2+$\frac{9}{4}$+$\frac{3}{2}$($\frac{1}{2}-λ$)t=[($\frac{1}{2}-λ$)t+$\frac{3}{4}$]2+$\frac{27}{16}$,
∴当($\frac{1}{2}$-λ)t=-$\frac{3}{4}$时即λ=$\frac{1}{2}$+$\frac{3}{4t}$时,$\overrightarrow{PE}$2取得最小值$\frac{27}{16}$.
∴$\overrightarrow{PE}$的最小值为$\frac{3\sqrt{3}}{4}$,此时λ=$\frac{1}{2}$+$\frac{3}{4t}$.
点评 本题考查了平面向量的基本定理,平面向量的应用,属于中档题.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{{\sqrt{7}}}{3}$ | B. | 3 | C. | $\frac{{\sqrt{11}}}{3}$ | D. | $\frac{{\sqrt{17}}}{3}$ |
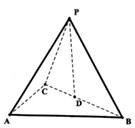 如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.
如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.