题目内容
10.若存在n∈N*使得(ax+1)2n和(x+a)2n+1(其中a≠0)的展开式中含xn项的系数相等,则a的最大值为$\frac{2}{3}$.分析 利用二项展开式的通项公式求出(ax+1)2n和(x+a)2n+1的展开式中含xn项的系数,根据已知条件得到关于a,n的方程;分离出a看成关于n的函数,通过函数的单调性,求出a的范围.
解答 解:设(x+a)2n+1的展开式为Tr+1,
则Tr+1=C2n+1rx2n+1-rar,
令2n+1-r=n,
得r=n+1,
所以xn的系数为C2n+1n+1an+1.
由C2n+1n+1mn+1=C2nnan,
得a=$\frac{n+1}{2n+1}$是关于n的减函数,
∵n∈N+,
∴$\frac{1}{2}$<a≤$\frac{2}{3}$,
故a的最大值为$\frac{2}{3}$,
故答案为:$\frac{2}{3}$.
点评 本题考查通过二项展开式的通项公式解决二项展开式的特定项问题,属于中档题

练习册系列答案
相关题目
1.下列函数是偶函数的是( )
| A. | y=tan3x | B. | y=cosx | C. | y=2sinx-1 | D. | y=2x |
18.某公司为了解下属某部门对企业职工的服务情况,随机访问50名职工.根据这50名职工对该部门的评分,得到的频率分布表如下:
(Ⅰ)求出频率分布表中m、n位置的相应数据,并画出频率分布直方图;
(Ⅱ)同一组中的数据用区间的中点值作代表,求这50名职工对该部门的评分的平均分.
| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.1 |
| [60,70) | m | 0.2 |
| [70,80) | 15 | n |
| [80,90) | 12 | 0.24 |
| 8 | 0.16 | |
| 合计 | 50 | 1 |
(Ⅱ)同一组中的数据用区间的中点值作代表,求这50名职工对该部门的评分的平均分.
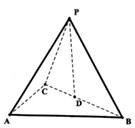 如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.
如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.