题目内容
12.已知不等式mx2-2mx-1<0.(1)若对于所有的实数x不等式恒成立,求m的取值范围;
(2)设不等式对于满足|m|≤1的一切m的值都成立,求x的取值范围.
分析 (1)通过讨论m的范围,结合二次函数的性质求出m的范围即可;
(2)根问题转化为$\left\{\begin{array}{l}{{-x}^{2}+2x-1<0}\\{{x}^{2}-2x-1<0}\end{array}\right.$,解不等式组即可.
解答 解:(1)m=0时,-1<0恒成立,
m≠0时,$\left\{\begin{array}{l}{m<0}\\{△={4m}^{2}+4m<0}\end{array}\right.$,解得:-1<m<0,
综上,m的范围是(-1,0];
(2)设f(m)=(x2-2x)m-1,
由题意得$\left\{\begin{array}{l}{f(-1)<0}\\{f(1)<0}\end{array}\right.$即$\left\{\begin{array}{l}{{-x}^{2}+2x-1<0}\\{{x}^{2}-2x-1<0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x≠1}\\{1-\sqrt{2}<x<1+\sqrt{2}}\end{array}\right.$,
∴1-$\sqrt{2}$<x<1或1<x<1+$\sqrt{2}$,
故x的范围是(1-$\sqrt{2}$,1)∪(1,1+$\sqrt{2}$).
点评 本题考查了二次函数的性质,考查绝对值问题,是一道中档题.

练习册系列答案
相关题目
3.若a-i与2+bi互为共轭复数,那么a+b等于( )
| A. | 3 | B. | 1 | C. | 0 | D. | 2 |
7.若函数$f(x)={log_a}({x^3}-ax)(a>0且a≠1)在区间(-\frac{1}{3},0)$内单调递增,则实数a的取值范围是( )
| A. | $[\frac{2}{3},1)$ | B. | $[\frac{1}{3},1)$ | C. | $[\frac{1}{3},1)∪(1,3]$ | D. | (1,3] |
17.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的一个焦点为F,以原点为圆心,OF为半径的圆与双曲线交于A,B,C,D四点,若四边形ABCD恰为正方形,且周长为6b,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{7}}}{3}$ | B. | 3 | C. | $\frac{{\sqrt{11}}}{3}$ | D. | $\frac{{\sqrt{17}}}{3}$ |
1.已知直线l1:(m+2)x-y+5=0与l2:(m+3)x+(18+m)y+2=0垂直,则实数m的值为( )
| A. | 2或4 | B. | 1或4 | C. | 1或2 | D. | -6或2 |
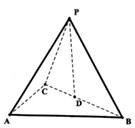 如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.
如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.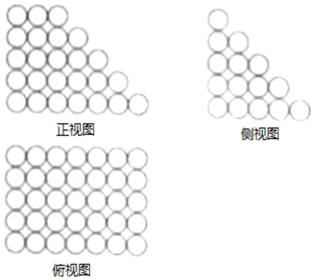 北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}[{({2b+d})a+({b+2d})c}]+\frac{n}{6}({c-a})$.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为85.
北宋数学家沈括的主要数学成就之一为隙积术,所谓隙积,即“积之有隙”者,如累棋、层坛之类,这种长方台形状的物体垛积.设隙积共n层,上底由长为a个物体,宽为b个物体组成,以下各层的长、宽依次各增加一个物体,最下层成为长为c个物体,宽为d个物体组成,沈括给出求隙积中物体总数的公式为S=$\frac{n}{6}[{({2b+d})a+({b+2d})c}]+\frac{n}{6}({c-a})$.已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示,则该垛积中所有小球的个数为85.