题目内容
11.已知双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为2c,直线l:y=kx-kc.若k=$\sqrt{3}$,则l与Γ的左、右两支各有一个交点;若k=$\sqrt{15}$,则l与Γ的右支有两个不同的交点,则Γ的离心率的取值范围为( )| A. | (1,2) | B. | (1,4) | C. | (2,4) | D. | (4,16) |
分析 由题意可知双曲线的渐近线斜率$\sqrt{3}$<$\frac{b}{a}$<$\sqrt{15}$,根据e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$,即可求得Γ的离心率的取值范围.
解答 解:由题意可知:直线l:y=k(x-c)过焦点F(c,0).双曲线的渐近线方程y=$\frac{b}{a}$x,
可得双曲线的渐近线斜率$\sqrt{3}$<$\frac{b}{a}$<$\sqrt{15}$,
∵e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$,
由3<$\frac{{b}^{2}}{{a}^{2}}$<15,4<1+$\frac{{b}^{2}}{{a}^{2}}$<16,
∴2<e<4,
∴双曲线离心率的取值范围为(2,4).
故选C.
点评 本题考查双曲线的离心率的范围,考查学生分析解决问题的能力,考查计算能力,属于中档题.

练习册系列答案
相关题目
1.下列函数是偶函数的是( )
| A. | y=tan3x | B. | y=cosx | C. | y=2sinx-1 | D. | y=2x |
16.复数$\frac{4}{1-i}$-$\frac{10}{3+i}$的共轭复数对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.若a-i与2+bi互为共轭复数,那么a+b等于( )
| A. | 3 | B. | 1 | C. | 0 | D. | 2 |
1.已知直线l1:(m+2)x-y+5=0与l2:(m+3)x+(18+m)y+2=0垂直,则实数m的值为( )
| A. | 2或4 | B. | 1或4 | C. | 1或2 | D. | -6或2 |
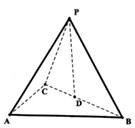 如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.
如图,三棱锥P-ABC中,D是BC的中点,△PAB为等边三角形,△ABC为等腰直角三角形,AB=AC=4,且二面角P-AB-D的余弦值为$\frac{\sqrt{3}}{3}$.