题目内容
12.双曲线x2-2y2=1的焦点坐标是( )| A. | $(\sqrt{3},0)$,$(-\sqrt{3},0)$ | B. | (1,0),(-1,0) | C. | $(-\frac{{\sqrt{6}}}{2},0)$,$(\frac{{\sqrt{6}}}{2},0)$ | D. | $(-\frac{{\sqrt{2}}}{2},0)$,$(\frac{{\sqrt{2}}}{2},0)$ |
分析 直接利用双曲线的方程求解焦点坐标即可.
解答 解:双曲线x2-2y2=1,可得a=1,b2=$\frac{1}{2}$,
∴c=$\frac{\sqrt{6}}{2}$,双曲线的焦点坐标是$(-\frac{\sqrt{6}}{2},0)$,$(\frac{\sqrt{6}}{2},0)$.
故选:C.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.如图,正方形ABCD中,E为DC的中点,若$\overrightarrow{AD}=λ\overrightarrow{AC}+μ\overrightarrow{AE}$,则λ-μ的值为( )
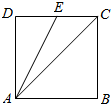

| A. | 3 | B. | 2 | C. | 1 | D. | -3 |
4.若f(x)对任意实数x恒有f(x)-2f(-x)=2x+1,则f(2)=( )
| A. | -$\frac{1}{3}$ | B. | 2 | C. | $\frac{1}{3}$ | D. | 3 |
2.已知A,B为圆x2+y2=2ax上的两点,若A,B关于直线y=2x+1对称,则实数a=( )
| A. | $-\frac{1}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点,$PO=\sqrt{2},AB=2$.求证:
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点,$PO=\sqrt{2},AB=2$.求证: