题目内容
20. 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点,$PO=\sqrt{2},AB=2$.求证:
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点,$PO=\sqrt{2},AB=2$.求证:(1)平面PAC⊥平面BDE;
(2)求二面角E-BD-C的大小.
分析 (I)利用线面、面面垂直的判定及其性质定理即可证明;
(2)如图所示,连接OE,OC.由(1)可知:BD⊥OC,BD⊥OE,可得∠COE是二面角E-BD-C的平面角.利用直角三角形的边角关系即可得出.
解答 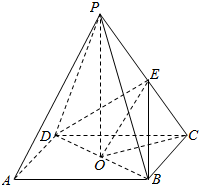 (Ⅰ)证明:∵PO⊥底面ABCD,∴PO⊥BD,
(Ⅰ)证明:∵PO⊥底面ABCD,∴PO⊥BD,
又∵AC⊥BD,且AC∩PO=O
∴BD⊥平面PAC,而BD?平面BDE,
∴平面PAC⊥平面BDE.
(2)如图所示,连接OE,OC.
由(1)可知:BD⊥OC,BD⊥OE,
∴∠COE是二面角E-BD-C的平面角.
∵AB=2,∴OC=$\frac{1}{2}$BD=$\sqrt{2}$.
∴OC=OP,
又PO⊥OC,PE=EC,
∴∠COE=45°.
点评 本题考查了线面、面面垂直的判定及其性质定理、空间角、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.函数y=$\frac{2}{{x}^{2}-9}$的定义域是( )
| A. | (-3,3) | B. | {-3,3} | C. | {x|x≠±3} | D. | (-∞,-3)∪(3,+∞) |
8.已知F1,F2分别是双曲线C:$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左,右焦点,M是C上的一点,且|MF2|=10,则|MF1|=( )
| A. | 10 | B. | 8 | C. | 4 | D. | 2 |
12.双曲线x2-2y2=1的焦点坐标是( )
| A. | $(\sqrt{3},0)$,$(-\sqrt{3},0)$ | B. | (1,0),(-1,0) | C. | $(-\frac{{\sqrt{6}}}{2},0)$,$(\frac{{\sqrt{6}}}{2},0)$ | D. | $(-\frac{{\sqrt{2}}}{2},0)$,$(\frac{{\sqrt{2}}}{2},0)$ |
10.已知M、N分别是四面体OABC的棱OA,BC的中点,P点在线段MN上,且MP=2PN,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
| A. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ |