题目内容
1.已知函数f(x)=|x-2|-|x+1|.(1)求证:-3≤f(x)≤3;
(2)解不等式f(x)≥x2-2x.
分析 (1)通过讨论x的范围得到相对应的f(x)的表达式,从而证明出结论;(2)利用分段函数解析式,分别解不等式,即可确定不等式的解集.
解答 解:(1)当x≤-1时,f(x)=3,成立;
当-1<x<2时,f(x)=-2x+1,
-4<-2x<2,∴-3<-2x+1<3,成立;
当x≥2时,f(x)=-3,成立;
故-3≤f(x)≤3;-------------------------(5分)
(2)当x≤-1时,x2-2x≤3,∴-1≤x≤2,∴x=1;
当-1<x<2时,x2-2x≤-2x+1,∴-1≤x≤1,∴-1<x≤1;
当x≥2时,x2-2x≤-3,无解;-------------------------(8分)
综合上述,不等式的解集为:[-1,1].-------------------------(10分)
点评 本题考查绝对值函数,考查分类讨论的数学思想,确定函数的解析式是关键.

练习册系列答案
相关题目
12.双曲线x2-2y2=1的焦点坐标是( )
| A. | $(\sqrt{3},0)$,$(-\sqrt{3},0)$ | B. | (1,0),(-1,0) | C. | $(-\frac{{\sqrt{6}}}{2},0)$,$(\frac{{\sqrt{6}}}{2},0)$ | D. | $(-\frac{{\sqrt{2}}}{2},0)$,$(\frac{{\sqrt{2}}}{2},0)$ |
10.已知M、N分别是四面体OABC的棱OA,BC的中点,P点在线段MN上,且MP=2PN,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
| A. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ |
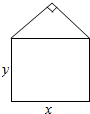 某单位用木料制作如图所示的框架,框架的下部是边长分别为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为4m2,问x,y分别为多少时用料最省?并求最省用料.
某单位用木料制作如图所示的框架,框架的下部是边长分别为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为4m2,问x,y分别为多少时用料最省?并求最省用料. 如图,四边形ABCD是圆O的内接四边形,延长BA和CD相交于点P,A是PB的一个三等点,D是PC的中点.
如图,四边形ABCD是圆O的内接四边形,延长BA和CD相交于点P,A是PB的一个三等点,D是PC的中点.