题目内容
3．如图，正方形ABCD中，E为DC的中点，若$\overrightarrow{AD}=λ\overrightarrow{AC}+μ\overrightarrow{AE}$，则λ-μ的值为（ ）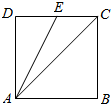
| A． | 3 | B． | 2 | C． | 1 | D． | -3 |
分析 利用平面向量的三角形法则，将$\overrightarrow{AD}$用$\overrightarrow{AC}，\overrightarrow{AE}$表示，再由平面向量基本定理得到λ，μ的值．
解答 解：由题意，因为E为DC的中点，所以$\overrightarrow{AE}=\frac{1}{2}（\overrightarrow{AD}+\overrightarrow{AC}）$，
所以$\overrightarrow{AD}=2\overrightarrow{AE}-\overrightarrow{AC}$，即$\overrightarrow{AD}=-\overrightarrow{AC}+2\overrightarrow{AD}$，所以λ=-1，μ=2，
所以λ-μ=-3；
故选：D．
点评 本题考查了三角形中线的向量性质以及平面向量基本定理的运用；属于基础题．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
11．函数f（x）=$\left\{\begin{array}{l}{x-2（x≤1）}\\{{x}^{2}+1（x＞1）}\end{array}\right.$，则f（3）=（ ）
| A． | 1 | B． | 4 | C． | 10 | D． | 2 |
18．已知等差数列{an}中，a1+a2+a3+…a100=0，则（ ）
| A． | a1+a101＞0 | B． | a2+a100＜0 | C． | a3+a98=0 | D． | a5=51 |
8．已知F1，F2分别是双曲线C：$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左，右焦点，M是C上的一点，且|MF2|=10，则|MF1|=（ ）
| A． | 10 | B． | 8 | C． | 4 | D． | 2 |
12．双曲线x2-2y2=1的焦点坐标是（ ）
| A． | $（\sqrt{3}，0）$，$（-\sqrt{3}，0）$ | B． | （1，0），（-1，0） | C． | $（-\frac{{\sqrt{6}}}{2}，0）$，$（\frac{{\sqrt{6}}}{2}，0）$ | D． | $（-\frac{{\sqrt{2}}}{2}，0）$，$（\frac{{\sqrt{2}}}{2}，0）$ |