题目内容
17.设函数f(x)=|x+1|+|x-4|-a.(1)当a=1时,求函数f(x)的最小值;
(2)若存在x∈N,使得f(x)≤a2-5a,求a的取值范围.
分析 (1)根据绝对值不等式的性质求出f(x)的最小值即可;(2)先求出f(x)的最小值,问题转化为5-a≤a2-5a,解出即可.
解答 解:(1)f(x)=|x+1|+|x-4|-1≥|x+1-x+4|-1=4,
故f(x)的最小值是4;
(2)由题意得只需f(x)min≤a2-5a即可,
而f(x)min=|x+1-x+4|-a=5-a,
即5-a≤a2-5a即可,
解不等式a2-4a-5≥0,
得:a≤-1或a≥5.
点评 本题考察了解绝对值不等式问题,考察函数恒成立问题,是一道基础题.

练习册系列答案
相关题目
8.已知F1,F2分别是双曲线C:$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左,右焦点,M是C上的一点,且|MF2|=10,则|MF1|=( )
| A. | 10 | B. | 8 | C. | 4 | D. | 2 |
12.双曲线x2-2y2=1的焦点坐标是( )
| A. | $(\sqrt{3},0)$,$(-\sqrt{3},0)$ | B. | (1,0),(-1,0) | C. | $(-\frac{{\sqrt{6}}}{2},0)$,$(\frac{{\sqrt{6}}}{2},0)$ | D. | $(-\frac{{\sqrt{2}}}{2},0)$,$(\frac{{\sqrt{2}}}{2},0)$ |
2.已知tanα=2,并且α为第三象限的角,那么cosα=( )
| A. | -$\frac{2\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | -$\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
7.已知点P(x,y)为圆x2+y2=1上的动点,则3x+4y的最小值为( )
| A. | 5 | B. | 1 | C. | 0 | D. | -5 |
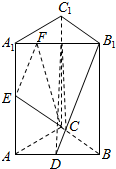 如图,在三棱柱ABC-A1B1C1中,D、E分别是AB、AA1的中点,AA1⊥平面ABC,AB⊥AC,AA1=4,AB=AC=2,且$\overrightarrow{{A}_{1}F}$=$\frac{1}{4}$$\overrightarrow{{A}_{1}{B}_{1}}$.
如图,在三棱柱ABC-A1B1C1中,D、E分别是AB、AA1的中点,AA1⊥平面ABC,AB⊥AC,AA1=4,AB=AC=2,且$\overrightarrow{{A}_{1}F}$=$\frac{1}{4}$$\overrightarrow{{A}_{1}{B}_{1}}$.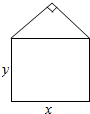 某单位用木料制作如图所示的框架,框架的下部是边长分别为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为4m2,问x,y分别为多少时用料最省?并求最省用料.
某单位用木料制作如图所示的框架,框架的下部是边长分别为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为4m2,问x,y分别为多少时用料最省?并求最省用料.