题目内容
20.某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为$\frac{2}{5}$,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{6}{125}$ | x | y | $\frac{24}{125}$ |
(2)求该生取得优秀成绩课程门数的数学期望Eξ.
分析 (1)由对立事件概率计算公式能求出该生至少有1门课程取得优秀成绩的概率,求出P(ξ=0)=$\frac{6}{125}$,P(ξ=3)=$\frac{24}{125}$,p<q,由此列出方程组能求出结果.
(2)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出该生取得优秀成绩课程门数的数学期望Eξ.
解答 解:(1)由已知得该生至少有1门课程取得优秀成绩的概率:
P=1-P(ξ=0)=1-$\frac{6}{125}$=$\frac{119}{125}$.
∵P(ξ=0)=$\frac{6}{125}$,P(ξ=3)=$\frac{24}{125}$,p<q,
∴$\left\{\begin{array}{l}{\frac{3}{5}(1-p)(1-q)=\frac{6}{125}}\\{\frac{2}{5}pq=\frac{24}{125}}\\{p<q}\end{array}\right.$,
解得p=$\frac{3}{5}$,q=$\frac{4}{5}$.
(2)由已知得ξ的可能取值为0,1,2,3,
P(ξ=0)=$\frac{6}{125}$,P(ξ=3)=$\frac{24}{125}$,
P(ξ=1)=$\frac{2}{5}(1-\frac{3}{5})(1-\frac{4}{5})$+(1-$\frac{2}{5}$)×$\frac{3}{5}×(1-\frac{4}{5})$+(1-$\frac{2}{5}$)×(1-$\frac{3}{5}$)×$\frac{4}{5}$=$\frac{37}{125}$,
P(ξ=2)=$\frac{2}{5}×\frac{3}{5}×(1-\frac{4}{5})$+$\frac{2}{5}×(1-\frac{3}{5})×\frac{4}{5}$+(1-$\frac{2}{5}$)×$\frac{3}{5}×\frac{4}{5}$=$\frac{58}{125}$,
∴Eξ=0×$\frac{6}{125}+1×\frac{37}{125}+2×\frac{58}{125}+3×\frac{24}{125}$=$\frac{9}{5}$.
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,考查推理论证能力、运算求解能力,考查分类讨论思想、转化化归思想、整体思想,是中档题.

| A. | y与x具有正的线性相关关系 | |
| B. | 若该大学某女生身高为170cm,则可断定其体重必为58.79kg | |
| C. | 过该大学某女生身高增加1cm,则其体重约增加0.85kg | |
| D. | 回归直线过样本的中心$(\overline x,\overline y)$ |
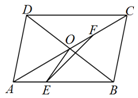 已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.
已知平行四边形ABCD中,$|\overrightarrow{AB}|=3$,$|\overrightarrow{AD}|=2$,对角线AC交BD于点O,AB上一点E满足$\overrightarrow{OE}•\overrightarrow{BD}=0$,F为AC上任意一点.