题目内容
9．（1+x-30x2）（2x-1）5的展开式中，含x3项的系数为-260（用数字填写答案）分析 分析x3得到所有可能情况，然后得到所求．
解答 解：（1+x-30x2）（2x-1）5的展开式中，含x3项为$1×{C}_{5}^{2}（2x）^{3}+x{C}_{5}^{3}（2x）^{2}（-1）^{3}$-30x2${C}_{5}^{4}（2x）（-1）^{4}$=80x3-40x3-300x3=-260x3，
所以x3的系数为-260；
故答案为：-260．
点评 本题考查了二项式定理；注意各种可能．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
19．已知集合A={0，2，4，6}，B={n∈N|2n＜8}，则集合A∩B的子集个数为（ ）
| A． | 8 | B． | 7 | C． | 6 | D． | 4 |
20．某同学参加学校自主招生3门课程的考试，假设该同学第一门课程取得优秀成绩概率为$\frac{2}{5}$，第二、第三门课程取得优秀成绩的概率分别为p，q（p＜q），且不同课程是否取得优秀成绩相互独立，记ξ为该生取得优秀成绩的课程数，其分布列为
（1）求该生至少有1门课程取得优秀成绩的概率及求p，q（p＜q）的值；
（2）求该生取得优秀成绩课程门数的数学期望Eξ．
| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{6}{125}$ | x | y | $\frac{24}{125}$ |
（2）求该生取得优秀成绩课程门数的数学期望Eξ．
4．如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该多面体的表面积为（ ）
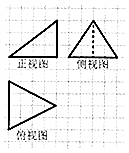
| A． | 20+3$\sqrt{2}$ | B． | 16+8$\sqrt{2}$ | C． | 18+3$\sqrt{5}$ | D． | 18+6$\sqrt{5}$ |
14．设E，F分别是正方形ABCD的边AB，BC上的点，且$AE=\frac{1}{2}AB$，$BF=\frac{2}{3}BC$，如果$\overrightarrow{EF}=m\overrightarrow{AB}+n\overrightarrow{AC}$（m，n为实数），那么m+n的值为（ ）
| A． | $-\frac{1}{2}$ | B． | 0 | C． | $\frac{1}{2}$ | D． | 1 |
1．如果执行如图的程序框图，且输入n=4，m=3，则输出的p=（ ）
| A． | 6 | B． | 24 | C． | 120 | D． | 720 |