题目内容
15.已知数列{an}中,${a_1}=1,{a_{n+1}}=2{a_n}+n-1({n∈{N^*}})$,则其前n项和Sn=${2^{n+1}}-2-\frac{{n({n+1})}}{2}$.分析 由已知求得a2=2,进一步得到数列{an-an-1+1}为等比数列,利用等比数列的通项公式可得an-an-1,再由“累加求和”方法可得an.再利用等比数列的求和公式即可得出.
解答 解:∵an+1=2an+n-1(n∈N*),a1=1,∴a2=2.
n≥2时,an=2an-1+n-2,
相减可得:an+1-an=2an-2an-1+1,
化为:an+1-an+1=2(an-an-1+1),
∴数列{an-an-1+1}为等比数列,首项为2,公比为2.
∴an-an-1+1=2×2n-1,∴an-an-1=2n-1.
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2n-1+2n-1-1+…+22-1+1
=$\frac{2(1-{2}^{n-1})}{1-2}-(n-1)+1$=2n-n.
∴其前n项和Sn=$\frac{2(1-{2}^{n})}{1-2}-\frac{n(n+1)}{2}$=${2^{n+1}}-2-\frac{{n({n+1})}}{2}$.
故答案为:${2^{n+1}}-2-\frac{{n({n+1})}}{2}$.
点评 本题考查了数列递推关系、等比数列的通项公式与求和公式、“累加求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.设p:x<3,q:-1<x<3,则¬q是¬p成立的( )
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
3.已知函数f(x)=x3+x2+mx+1在区间(-1,2)上不是单调函数,则实数m的取值范围是( )
| A. | (-∞,-16)∪($\frac{1}{3}$,+∞) | B. | [-16,$\frac{1}{3}$] | C. | (-16,$\frac{1}{3}$) | D. | ($\frac{1}{3}$,+∞) |
20.某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为$\frac{2}{5}$,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
(1)求该生至少有1门课程取得优秀成绩的概率及求p,q(p<q)的值;
(2)求该生取得优秀成绩课程门数的数学期望Eξ.
| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{6}{125}$ | x | y | $\frac{24}{125}$ |
(2)求该生取得优秀成绩课程门数的数学期望Eξ.
4.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的表面积为( )
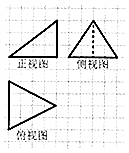

| A. | 20+3$\sqrt{2}$ | B. | 16+8$\sqrt{2}$ | C. | 18+3$\sqrt{5}$ | D. | 18+6$\sqrt{5}$ |