题目内容
12.已知集合$A=\left\{{y|y=\sqrt{3-2x},x∈[{-\frac{13}{2},\frac{3}{2}}]}\right\}$,B={x|1-m≤x≤m+1}.(1)若m=2,求A∩B;
(2)若B⊆A,求m的取值范围.
分析 (1)若m=2,求出集合A,B,即可求A∩B;
(2)若B⊆A,分类讨论,求m的取值范围.
解答 解:$A=\left\{{y|y=\sqrt{3-2x},x∈[{-\frac{13}{2},\frac{3}{2}}]}\right\}$=[0,4]
(1)m=2,B={x|-1≤x≤3},
∴A∩B=[0,3];
(2)B⊆A,则B=∅,1-m>m+1,∴m<0,
B≠∅,$\left\{\begin{array}{l}{1-m≤m+1}\\{1-m≥0}\\{m+1≤4}\end{array}\right.$,∴0≤m≤1,
综上所述,m≤1.
点评 本题考查集合的关系与运算,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
3.已知函数f(x)=x3+x2+mx+1在区间(-1,2)上不是单调函数,则实数m的取值范围是( )
| A. | (-∞,-16)∪($\frac{1}{3}$,+∞) | B. | [-16,$\frac{1}{3}$] | C. | (-16,$\frac{1}{3}$) | D. | ($\frac{1}{3}$,+∞) |
20.某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为$\frac{2}{5}$,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
(1)求该生至少有1门课程取得优秀成绩的概率及求p,q(p<q)的值;
(2)求该生取得优秀成绩课程门数的数学期望Eξ.
| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{6}{125}$ | x | y | $\frac{24}{125}$ |
(2)求该生取得优秀成绩课程门数的数学期望Eξ.
4.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的表面积为( )
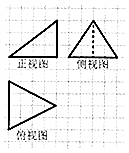

| A. | 20+3$\sqrt{2}$ | B. | 16+8$\sqrt{2}$ | C. | 18+3$\sqrt{5}$ | D. | 18+6$\sqrt{5}$ |
1.如果执行如图的程序框图,且输入n=4,m=3,则输出的p=( )


| A. | 6 | B. | 24 | C. | 120 | D. | 720 |
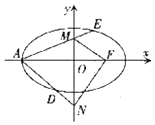 已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左顶点为A,右焦点为F,O为原点,M,N是y轴上的两个动点,且MF⊥NF,直线AM和AN分别与椭圆C交于E,D两点.
已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左顶点为A,右焦点为F,O为原点,M,N是y轴上的两个动点,且MF⊥NF,直线AM和AN分别与椭圆C交于E,D两点.