题目内容
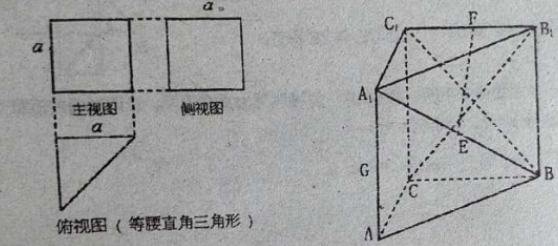
一个三棱锥的三视图及直观图如图所示,E,F,G分别是A1B,B1C1,AA1的中点,AA1⊥底面ABC
(1)求四棱锥B-ACC1A1的体积;
(2)求证:B1C⊥平面A1BC1;
(3)求证:EF∥平面ACC1A1
 .
.
(1)求四棱锥B-ACC1A1的体积;
(2)求证:B1C⊥平面A1BC1;
(3)求证:EF∥平面ACC1A1
 .
.考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由已知中的三视图,我们易得到这是一个底面为等腰直角三角形的直三棱柱,且底面直角边和棱柱高均为a,代入棱柱体积公式,即可得到答案.
(2)连AB1,AC1,由矩形的性质及三角形中位线定理,易得MN∥AC1,再由线面平行的判定定理,即可得到MN∥平面AA1C1C;
(2)连AB1,AC1,由矩形的性质及三角形中位线定理,易得MN∥AC1,再由线面平行的判定定理,即可得到MN∥平面AA1C1C;
解答:
解:(1)如图可知,在这个多面体的直观图中,
AA1⊥平面ABC,且AB⊥AC,AB=AC=CC1=a,
所以V=
a2×a=
a3;
(2)由三视图得到几何体是直三棱柱,并且底面是等腰直角三角形,
所以A1C1⊥面BCC1B1,所以A1C1⊥B1C,又四边形BCC1B1为正方形,所以B1C⊥BC1,
所以AB1C⊥平面A1BC1
(3)连AB1,AC1,由矩形性质得:AB1与A1B交于点E,
在△AB1C1中,由中位线性质得EF∥AC1,
又因为EF?平面AA1C1C,
所以EF∥平面AA1C1C.
AA1⊥平面ABC,且AB⊥AC,AB=AC=CC1=a,
所以V=
| 1 |
| 2 |
| 1 |
| 2 |
(2)由三视图得到几何体是直三棱柱,并且底面是等腰直角三角形,
所以A1C1⊥面BCC1B1,所以A1C1⊥B1C,又四边形BCC1B1为正方形,所以B1C⊥BC1,
所以AB1C⊥平面A1BC1
(3)连AB1,AC1,由矩形性质得:AB1与A1B交于点E,
在△AB1C1中,由中位线性质得EF∥AC1,
又因为EF?平面AA1C1C,
所以EF∥平面AA1C1C.
点评:本题考查的知识点是直线与平面平等的判定,直线与平面垂直的判定,其中熟练掌握空间直线与平面平行及垂直的判定定理,性质定理、定义及几何特征,建立良好的空间想像能力是解答本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
若两个二面角的面分别垂直且它们的棱互相平行,则它们的角度之间的关系为( )
| A、相等 | B、互补 |
| C、相等或互补 | D、无法确定 |