题目内容
P:x2-x-20≤0,Q:x2-2x+1一m2≤0,若P是Q的充分不必要条件,求m的范围.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:首先,根据P:x2-8x-20≤0,得-2≤x≤10,根据Q:x2-2x+1-m2≤0,得[x-(1+m)][x-(1-m)]≤0,然后,对m的取值情况进行讨论.
解答:
解:根据P:x2-8x-20≤0,得
-2≤x≤10,
根据Q:x2-2x+1-m2≤0,得
[x-(1+m)][x-(1-m)]≤0,①
当m=0时,根据不等式①得到x=1,显然不满足条件,
当m>0时,根据不等式①得,
1-m≤m≤1+m,
∵P是Q的充分不必要条件,
∴
,
∴
,
∴m≥9.
当m<0时,根据不等式①得,
1+m≤m≤1-m,
∵P是Q的充分不必要条件,
,
∴
,
∴m≤-9,
∴m的范围(-∞,-9]∪[9,+∞).
-2≤x≤10,
根据Q:x2-2x+1-m2≤0,得
[x-(1+m)][x-(1-m)]≤0,①
当m=0时,根据不等式①得到x=1,显然不满足条件,
当m>0时,根据不等式①得,
1-m≤m≤1+m,
∵P是Q的充分不必要条件,
∴
|
∴
|
∴m≥9.
当m<0时,根据不等式①得,
1+m≤m≤1-m,
∵P是Q的充分不必要条件,
|
∴
|
∴m≤-9,
∴m的范围(-∞,-9]∪[9,+∞).
点评:本题重点考查了充分条件、必要条件、充要条件的判断和应用,属于中档题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
观察如图所示的四个几何体:(1)a是棱台;(2)b是圆台;(3)c是棱锥;(4)d不是棱柱.其中判断正确的是( )
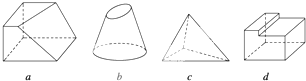

| A、(1)(2) | B、(3)(4) |
| C、(3) | D、(4) |
 .
.