题目内容
命题p:方程
+
=1(k∈R)表示双曲线;
命题q:不等式kx2+kx+1>0的解集为R;
若命题p∨q为真命题,p∧q为假命题,求实数k的取值范围.
| x2 |
| k-3 |
| y2 |
| k+3 |
命题q:不等式kx2+kx+1>0的解集为R;
若命题p∨q为真命题,p∧q为假命题,求实数k的取值范围.
考点:命题的真假判断与应用
专题:简易逻辑
分析:由方程
+
=1(k∈R)表示双曲线求出k的范围,由不等式kx2+kx+1>0的解集为R求出k的范围,然后由p∨q为真命题,p∧q为假命题得到p,q的真假情况,转化为集合间的关系得答案.
| x2 |
| k-3 |
| y2 |
| k+3 |
解答:
解:方程
+
=1(k∈R)表示双曲线,则(k-3)(k+3)<0,即-3<k<3.
不等式kx2+kx+1>0的解集为R?k=0或
,解得:0≤k<4.
命题p∨q为真命题,p∧q为假命题,说明p、q一真一假.
若p真q假:则k的范围是{k|k<0或k≥4}∩{k|-3<k<3}=(-3,0);
若p假q真:则k的范围是{k|k≤-3或k≥3}∩{k|0≤k<4}=[3,4).
综上,k的取值范围是:(-3,0)∪[3,4).
| x2 |
| k-3 |
| y2 |
| k+3 |
不等式kx2+kx+1>0的解集为R?k=0或
|
命题p∨q为真命题,p∧q为假命题,说明p、q一真一假.
若p真q假:则k的范围是{k|k<0或k≥4}∩{k|-3<k<3}=(-3,0);
若p假q真:则k的范围是{k|k≤-3或k≥3}∩{k|0≤k<4}=[3,4).
综上,k的取值范围是:(-3,0)∪[3,4).
点评:本题考查了命题的真假判断与应用,体现了数学转化思想方法,训练了补集思想在解题中的应用,是中档题.

练习册系列答案
相关题目
一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积是( )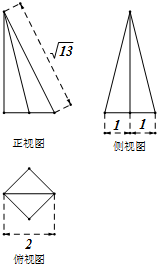

| A、2 | ||||
B、3
| ||||
C、3
| ||||
D、3
|
双曲线
-
=1的焦点到渐近线的距离为( )
| x2 |
| 4 |
| y2 |
| 12 |
A、2
| ||
| B、2 | ||
C、
| ||
| D、1 |
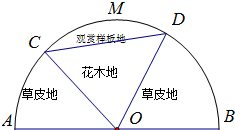 某园林公司计划在一块O为圆心,R(R为常数)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
某园林公司计划在一块O为圆心,R(R为常数)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
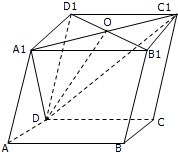 如图所示,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证:
如图所示,在平行六面体ABCD-A1B1C1D1中,O是B1D1的中点,求证: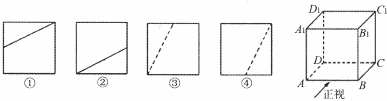
 某几何体的三视图如图所示,其中正视图和左视图的上半部分均为边长为2的等边三角形,则该几何体的体积为
某几何体的三视图如图所示,其中正视图和左视图的上半部分均为边长为2的等边三角形,则该几何体的体积为