Question

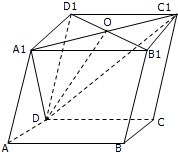如图所示，在平行六面体ABCD-A₁B₁C₁D₁中，O是B₁D₁的中点，求证：

B1C

、

OD

、

OC1

是共面向量．

Answer 1

考点：空间向量的基本定理及其意义

专题：空间向量及应用

分析：在平行六面体ABCD-A₁B₁C₁D₁中，先判断

OD

、

OC1

是共面向量，再判断

B1C

，与

OD

、

OC1

是共面向量即可．

解答： 解：证明，在平行六面体ABCD-A₁B₁C₁D₁中，O是B₁D₁的中点，
∴

OD

、

OC1

是共面向量；
即OD?平面OC₁D，OC₁?平面OC₁D；
又∵A₁B₁∥AB，且A₁B₁=AB，AB∥DC，且AB=DC，
∴A₁B₁∥DC，且A₁B₁=DC；
∴四边形A₁B₁CD是平行四边形；
∴A₁D∥B₁C，
∴

A1D

∥

B1C

，
又A₁D?平面OC₁D，
∴

B1C

与

OD

、

OC1

是共面向量．

点评：本题考查空间向量的应用问题，解题时应根据向量共面的条件进行证明，是基础题．