Question

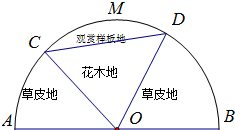某园林公司计划在一块O为圆心，R（R为常数）为半径的半圆形（如图）地上种植花草树木，其中弓形CMDC区域用于观赏样板地，△OCD区域用于种植花木出售，其余区域用于种植草皮出售．已知观赏样板地的成本是每平方米2元，花木的利润是每平方米8元，草皮的利润是每平方米3元．
（1）设∠COD=θ，

CMD

=l，分别用θ，l表示弓形CMDC的面积S_弓=f（θ），S_弓=g（l）；
（2）园林公司应该怎样规划这块土地，才能使总利润最大？（参考公式：扇形面积公式S=

1

2

R²θ=Rl）

Answer 1

考点：导数在最大值、最小值问题中的应用

专题：计算题,应用题,函数的性质及应用,导数的综合应用

分析：（1）利用扇形面积公式及三角形面积公式写出弓形面积；
（2）设总利润为y元，草皮利润为y₁元，花木地利润为y₂元，观赏样板地成本为y₃元；则y1=3(

1

2

πR2-

1

2

lR)，y2=

1

2

R2sinθ•8，y3=

1

2

R(l-Rsinθ)•2，则y=y1+y2-y3=3(

1

2

πR2-

1

2

R2θ)+

1

2

R2sinθ•8-

1

2

R2(θ-sinθ)•2．=

1

2

R2[3π-(5θ-10sinθ)]；利用导数求最值．

解答： 解：（1）∵S扇=

1

2

R2θ，S△OCD=

1

2

R2sinθ，
∴S弓=f(θ)=

1

2

R2(θ-sinθ)．
又∵S扇=

1

2

Rl，S△OCD=

1

2

R2sin

l

R

，
∴S弓=g(l)=

1

2

R(l-Rsin

l

R

)．
（2）设总利润为y元，草皮利润为y₁元，花木地利润为y₂元，观赏样板地成本为y₃元；
则y1=3(

1

2

πR2-

1

2

lR)，y2=

1

2

R2sinθ•8，y3=

1

2

R(l-Rsinθ)•2，
∴y=y1+y2-y3=3(

1

2

πR2-

1

2

R2θ)+

1

2

R2sinθ•8-

1

2

R2(θ-sinθ)•2．=

1

2

R2[3π-(5θ-10sinθ)]．
设g（θ）=5θ-10sinθ，θ∈（0，π）．
g′（θ）=5-10cosθ，
由g′(θ)＜0，cosθ＞

1

2

，g(θ)在θ∈(0，

π

3

)上为减函数；
由g′(θ)＞0，cosθ＜

1

2

，g(θ)在θ∈(

π

3

，π)上为增函数．
当θ=

π

3

时，g（θ）取到最小值，此时总利润最大．
所以当园林公司把扇形的圆心角设计成

π

3

时，总利润最大．

点评：本题考查导数，函数性质，考查运算能力和分析问题和解决问题的能力．