题目内容
巳知双曲线G的中心在坐标原点,实轴在x轴上,离心率为
,且G上一点到G的两个焦点的距离之差为12,则双曲线G的方程为( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:设双曲线G的方程为
-
=1,由已知得
,由此能求出双曲线方程.
| x2 |
| a2 |
| y2 |
| b2 |
|
解答:
解:设双曲线G的方程为
-
=1,
∵离心率为
,且G上一点到G的两个焦点的距离之差为12,
∴
,解得a=6,b=3,
∴所求双曲线方程为
-
=1.
故选:B.
| x2 |
| a2 |
| y2 |
| b2 |
∵离心率为
| ||
| 2 |
∴
|
∴所求双曲线方程为
| x2 |
| 36 |
| y2 |
| 9 |
故选:B.
点评:本题考查双曲线方程的求法,是中档题,解题时要注意双曲线性质的合理运用.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知函数f(x)=
+
的两个极值点分别为x1,x2,且x1∈(0,1),x2∈(1,+∞),点P(m,n)表示的平面区域为D,若函数y=loga(x+4)(a>1)的图象上存在区域D内的点,则实数a的取值范围为( )
| x3 |
| 3 |
| mx2+(m+n)x+1 |
| 2 |
| A、(1,3] |
| B、(1,3) |
| C、(3,+∞) |
| D、[3,+∞) |
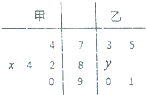 某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.
某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.