题目内容
已知函数f(x)=
+
的两个极值点分别为x1,x2,且x1∈(0,1),x2∈(1,+∞),点P(m,n)表示的平面区域为D,若函数y=loga(x+4)(a>1)的图象上存在区域D内的点,则实数a的取值范围为( )
| x3 |
| 3 |
| mx2+(m+n)x+1 |
| 2 |
| A、(1,3] |
| B、(1,3) |
| C、(3,+∞) |
| D、[3,+∞) |
考点:简单线性规划,复合命题的真假
专题:数形结合,函数的性质及应用,导数的综合应用
分析:求出函数f(x)的导函数,由原函数的两个极值点分别在(0,1),(1,+∞)内列式得到m,n的关系,作出可行域,由函数y=loga(x+4)(a>1)的图象上存在区域D内的点得到对数不等式,求解不等式得实数a的取值范围.
解答:
解:∵函数f(x)=
+
的两个极值点分别为x1,x2,
且x1∈(0,1),x2∈(1,+∞),
∴y′=x2+mx+
=0的两根x1,x2满足0<x1<1<x2,
则x1+x2=-m,x1x2=
>0,
(x1-1)(x2-1)=x1x2-(x1+x2)+1=
+m+1<0,
即n+3m+2<0,
∴-m<n<-3m-2,
作平面区域如图:
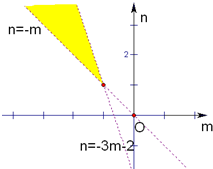
∴m<-1,n>1.
∵y=loga(x+4)(a>1)的图象上存在区域D内的点,
∴loga(-1+4)>1,即
>1,
∵a>1,∴lga>0,
∴1g3>lga.
解得1<a<3.
故选:B.
| x3 |
| 3 |
| mx2+(m+n)x+1 |
| 2 |
且x1∈(0,1),x2∈(1,+∞),
∴y′=x2+mx+
| m+n |
| 2 |
则x1+x2=-m,x1x2=
| m+n |
| 2 |
(x1-1)(x2-1)=x1x2-(x1+x2)+1=
| m+n |
| 2 |
即n+3m+2<0,
∴-m<n<-3m-2,
作平面区域如图:

∴m<-1,n>1.
∵y=loga(x+4)(a>1)的图象上存在区域D内的点,
∴loga(-1+4)>1,即
| lg3 |
| lga |
∵a>1,∴lga>0,
∴1g3>lga.
解得1<a<3.
故选:B.
点评:本题考查了利用导数研究函数的极值,考查了简单的线性规划,体现了数学转化思想方法和数形结合的解题思想方法,是中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
在△ABC中,内角A,B,C所对的边分别是a,b,c,已知b-c=
a,2sinB=3sinC,则cosA=( )
| 1 |
| 4 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
若直线l过点A(0,a),斜率为1,圆x2+y2=4上恰有1个点到l的距离为1,则a的值为( )
A、3
| ||
B、±3
| ||
| C、±2 | ||
D、±
|
函数y=2x-x2的图象大致是( )
A、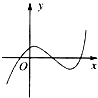 |
B、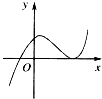 |
C、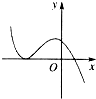 |
D、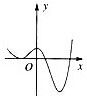 |
函数f(x)=
,则
f(x)dx的值为( )
|
| ∫ | 2 -2 |
| A、π+6 | B、π-2 | C、2π | D、8 |
巳知双曲线G的中心在坐标原点,实轴在x轴上,离心率为
,且G上一点到G的两个焦点的距离之差为12,则双曲线G的方程为( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
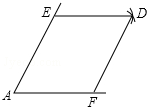 如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.