题目内容
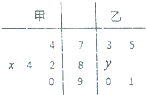 某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.
某中学高二年级的甲、乙两个班中,需根据某次数学预赛成绩选出某班的5名学生参加数学竞赛决赛,已知这次预赛他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班5名学生成绩的平均分是83,乙班5名学生成绩的中位数是86.(Ⅰ)求出x,y的值,且分别求甲、乙两个班中5名学生成绩的方差S12、S22,并根据结果,你认为应该选派哪一个班的学生参加决赛?
(Ⅱ)从成绩在85分及以上的学生中随机抽取2名.求至少有1名来自甲班的概率.
考点:古典概型及其概率计算公式,茎叶图
专题:概率与统计
分析:(Ⅰ)由题意知求出x=5,y=6.从而求出乙班学生的平均数为83,分别求出S12和S22,根据甲、乙两班的平均数相等,甲班的方差小,得到应该选派甲班的学生参加决赛.
(Ⅱ)成绩在85分及以上的学生一共有5名,其中甲班有2名,乙班有3名,由此能求出随机抽取2名,至少有1名来自甲班的概率.
(Ⅱ)成绩在85分及以上的学生一共有5名,其中甲班有2名,乙班有3名,由此能求出随机抽取2名,至少有1名来自甲班的概率.
解答:
解:(Ⅰ)由题意知
,
解得x=5,y=6.
乙班学生的平均数
=
(73+75+86+90+91)=83,
S12=
[(74-83)2+(82-83)2+(84-83)2+(85-83)2+(90-83)2]=35.2,
S22=
[(73-83)2+(75-83)2+(86-83)2+(90-83)2+(91-83)2]=73.2,
∵甲、乙两班的平均数相等,甲班的方差小,
∴应该选派甲班的学生参加决赛.
(Ⅱ)成绩在85分及以上的学生一共有5名,其中甲班有2名,乙班有3名,
随机抽取2名,至少有1名来自甲班的概率:
P=1-
=0.7.
|
解得x=5,y=6.
乙班学生的平均数
. |
| y |
| 1 |
| 5 |
S12=
| 1 |
| 5 |
S22=
| 1 |
| 5 |
∵甲、乙两班的平均数相等,甲班的方差小,
∴应该选派甲班的学生参加决赛.
(Ⅱ)成绩在85分及以上的学生一共有5名,其中甲班有2名,乙班有3名,
随机抽取2名,至少有1名来自甲班的概率:
P=1-
| ||
|
点评:本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
巳知双曲线G的中心在坐标原点,实轴在x轴上,离心率为
,且G上一点到G的两个焦点的距离之差为12,则双曲线G的方程为( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若定义在R上的函数f(x)满足:对任意x1,x2∈R有f(x1+x2)=f(x1)+f(x2)+1,则下列说法一定正确的是( )
| A、f(x)-1是奇函数 |
| B、f(x)-1是偶函数 |
| C、f(x)+1是奇函数 |
| D、f(x)+1是偶函数 |
方程x2+y2+2ax+2by+a2+b2=0表示的图形是( )
| A、以(a,b)为圆心的圆 |
| B、以(-a,-b)为圆心的圆 |
| C、点(a,b) |
| D、点(-a,-b) |
函数f(x)=
的定义域为( )
| lg(x2-1) | ||
|
| A、(-∞,-2)∪(1,+∞) |
| B、(-2,1) |
| C、(-∞,-1)∪(2,+∞) |
| D、(1,2) |