题目内容
设函数f(x)=asinx+bcosx(a、b为常数).
(1)若f(
)=0,f(π)=
,求f(x)的解析式,并化为f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的形式;
(2)若a=2,b=0,g(x)=f(x+
),写出g(x)的解析式;当x∈[-
,
]时,按照“五点法”作图步骤,画出函数g(x)的图象,写出一个区间D,D⊆[-
,
],使得在区间D上,g(x)≥0且g(x)单调递减.
(1)若f(
| π |
| 4 |
| 2 |
| π |
| 2 |
(2)若a=2,b=0,g(x)=f(x+
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,五点法作函数y=Asin(ωx+φ)的图象
专题:三角函数的图像与性质
分析:(1)由已知联立方程组求解a,b的值,代入后化积得答案;
(2)在f(x)=asinx+bcosx中取a=2,b=0得到f(x),平移后得到g(x),由五点作图得到函数图象,由图象求得满足条件的减区间.
(2)在f(x)=asinx+bcosx中取a=2,b=0得到f(x),平移后得到g(x),由五点作图得到函数图象,由图象求得满足条件的减区间.
解答:
解:(1)由f(x)=asinx+bcosx,且f(
)=0,f(π)=
,得
,解得:a=
,b=-
.
∴f(x)=
sinx-
cosx=2sin(x-
);
(2)若a=2,b=0,则f(x)=2sinx,
g(x)=f(x+
)=2sin(x+
),
画函数g(x)=2sin(x+
)在x∈[-
,
]上的图象步骤如下:
列表:
描点并用平滑曲线连接:

由图可知满足条件的区间D为:[
,
].
| π |
| 4 |
| 2 |
|
| 2 |
| 2 |
∴f(x)=
| 2 |
| 2 |
| π |
| 4 |
(2)若a=2,b=0,则f(x)=2sinx,
g(x)=f(x+
| π |
| 6 |
| π |
| 6 |
画函数g(x)=2sin(x+
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
列表:
| x | -
|
|
|
|
| ||||||||||
x+
| 0 |
| π |
| 2π | ||||||||||
| g(x) | 0 | 2 | 0 | -2 | 0 |

由图可知满足条件的区间D为:[
| π |
| 3 |
| 5π |
| 6 |
点评:本题考查了由已知条件求解三角函数的图象,考查了五点作图法作三角函数的图象,训练了复合函数单调性的求法,是中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
函数y=2x-x2的图象大致是( )
A、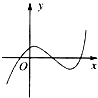 |
B、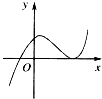 |
C、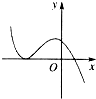 |
D、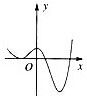 |
函数f(x)=
,则
f(x)dx的值为( )
|
| ∫ | 2 -2 |
| A、π+6 | B、π-2 | C、2π | D、8 |
巳知双曲线G的中心在坐标原点,实轴在x轴上,离心率为
,且G上一点到G的两个焦点的距离之差为12,则双曲线G的方程为( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=f′(x)的图象如图所示,则关于函数y=f(x)的说法正确的是( )


| A、函数y=f(x)有3个极值点 |
| B、函数y=f(x)在区间(-∞,-4)单调递减 |
| C、函数y=f(x)在区间(-2,+∞)单调递增 |
| D、x=1时函数y=f(x)取极大值 |
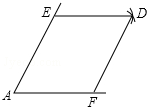 如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.