题目内容

8．已知a，b，c为正实数，且a3+b3+c3=a2b2c2，求证：a+b+c≥3$\root{3}{3}$．

分析 利用基本不等式的性质进行证明．

解答 证明：∵a3+b3+c3=a2b2c2，a3+b3+c3≥3abc，
∴a2b2c2≥3abc，∴abc≥3，
∴a+b+c≥3$\root{3}{abc}$≥3$\root{3}{3}$．
当且仅当a=b=c=$\root{3}{3}$时，取“=”．

点评 本题考查了不等式的证明，基本不等式的应用，属于中档题．

练习册系列答案
相关题目
18．已知函数$f（x）=\frac{a}{x-2}+lnx$，其中a∈R．
（Ⅰ）给出a的一个取值，使得曲线y=f（x）存在斜率为0的切线，并说明理由；
（Ⅱ）若f（x）存在极小值和极大值，证明：f（x）的极小值大于极大值．
19．已知集合A={x|1＜2x≤16}，B={x|x＜a}，若A∩B=A，则实数a的取值范围是（　　）
A．a＞4B．a≥4C．a≥0D．a＞0
16．设a，b∈R，$\frac{1+i}{1-i}$=a+bi（i为虚数单位），则b的值为1．
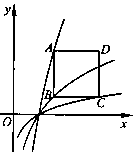3．如图，已知正方形ABCD的边长为2，BC平行于x轴，顶点A，B和C分别在函数y1=3logax，y2=2logax和y3=logax（a＞1）的图象上，则实数a的值为$\sqrt{2}$．
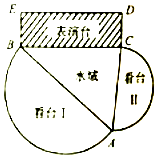13．在同一直角坐标系中，函数$y=sin（{x+\frac{π}{3}}）（{x∈[{0，2π}）}）$的图象和直线y=$\frac{1}{2}$的交点的个数是2．
20．在水域上建一个演艺广场，演艺广场由看台Ⅰ，看台Ⅱ，三角形水域ABC，及矩形表演台BCDE四个部分构成（如图），看台Ⅰ，看台Ⅱ是分别以AB，AC为直径的两个半圆形区域，且看台Ⅰ的面积是看台Ⅱ的面积的3倍，矩形表演台BCDE 中，CD=10米，三角形水域ABC的面积为$400\sqrt{3}$平方米，设∠BAC=θ．
（1）求BC的长（用含θ的式子表示）；
（2）若表演台每平方米的造价为0.3万元，求表演台的最低造价．
17．为了得到函数y=cos2x的图象，只要把函数$y=sin（2x-\frac{π}{3}）$的图象上所有的点（　　）
A．向右平行移动$\frac{5π}{12}$个单位长度B．向左平行移动$\frac{5π}{12}$个单位长度
C．向右平行移动$\frac{5π}{6}$个单位长度D．向左平行移动$\frac{5π}{6}$个单位长度
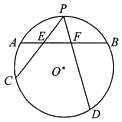12．如图，已知AB为圆O的一条弦，点P为弧$\widehat{AB}$的中点，过点P任作两条弦PC，PD分别交AB于点E，F
求证：PE•PC=PF•PD．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网