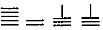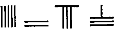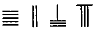题目内容
13.在同一直角坐标系中,函数$y=sin({x+\frac{π}{3}})({x∈[{0,2π})})$的图象和直线y=$\frac{1}{2}$的交点的个数是2.分析 令y=sin(x+$\frac{π}{3}$)=$\frac{1}{2}$,求出在x∈[0,2π)内的x值即可.
解答 解:令y=sin(x+$\frac{π}{3}$)=$\frac{1}{2}$,
解得x+$\frac{π}{3}$=$\frac{π}{6}$+2kπ,
或x+$\frac{π}{3}$=$\frac{5π}{6}$+2kπ,k∈Z;
即x=-$\frac{π}{6}$+2kπ,
或x=$\frac{π}{2}$+2kπ,k∈Z;
∴同一直角坐标系中,函数y的图象和直线y=$\frac{1}{2}$
在x∈[0,2π)内的交点为($\frac{π}{2}$,$\frac{1}{2}$)和($\frac{11π}{6}$,$\frac{1}{2}$),共2个.
故答案为:2.
点评 本题考查了正弦函数的图象与性质的应用问题,是基础题.

练习册系列答案
相关题目
4.已知函数f(x)=sin(x+φ)-2cos(x+φ)(0<φ<π)的图象关于直线x=π对称,则cos2φ=( )
| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
2.若不等式ln(x+2)+a(x2+x)≥0对于任意的x∈[-1,+∞)恒成立,则实数a的取值范围是( )
| A. | [0,+∞) | B. | [0,1] | C. | [0,e] | D. | [-1,0] |
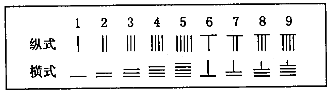
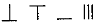 ,则5288用算筹式可表示为( )
,则5288用算筹式可表示为( )