题目内容
12.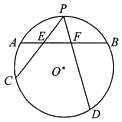 如图,已知AB为圆O的一条弦,点P为弧$\widehat{AB}$的中点,过点P任作两条弦PC,PD分别交AB于点E,F
如图,已知AB为圆O的一条弦,点P为弧$\widehat{AB}$的中点,过点P任作两条弦PC,PD分别交AB于点E,F求证:PE•PC=PF•PD.
分析 连结PA、PB、CD、BC,推导出∠PFE=∠PBA+∠DPB=∠PCB+∠DCB=∠PCD,从而E、F、D、C四点共圆.由此能证明PE•PC=PF•PD.
解答 解:连结PA、PB、CD、BC,
因为∠PAB=∠PCB,又点P为弧AB的中点,
所以∠PAB=∠PBA,
所以∠PCB=∠PBA,
又∠DCB=∠DPB,
所以∠PFE=∠PBA+∠DPB=∠PCB+∠DCB=∠PCD,
所E、F、D、C四点共圆.
所以PE•PC=PF•PD.
点评 本题考查两组线段乘积相等的证明,考查弦切角、切割线定理、圆等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,数形结合思想,考查创新意识、应用意识,是中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
3.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)中,F1,F2为左,右焦点,以F1,F2为直径的圆与椭圆在第一、三象限的交点分别为A、B,若直线AB与直线x+$\sqrt{3}$y-7=0互相垂直,则椭圆的离心率为( )
| A. | $\frac{\sqrt{3}+1}{2}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\sqrt{3}$-1 | D. | $\frac{\sqrt{5}-1}{2}$ |
20.已知点A(-4,0),B(-1,0),C(-4,3),动点P、Q满足$\frac{|PA|}{|PB|}$=$\frac{|QA|}{|QB|}$=2,则|$\overrightarrow{CP}$+$\overrightarrow{CQ}$|取值范围是 ( )
| A. | [1,16] | B. | [6,14] | C. | [4,16] | D. | [$\sqrt{13}$,3$\sqrt{5}$] |
2.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,若$\overrightarrow{b}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=2,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |