Question

3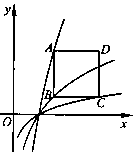．如图，已知正方形ABCD的边长为2，BC平行于x轴，顶点A，B和C分别在函数y₁=3log_ax，y₂=2log_ax和y₃=log_ax（a＞1）的图象上，则实数a的值为$\sqrt{2}$．

Answer 1

分析 设B（x，2log_ax），利用BC平行于x轴得出C（x²，2log_ax），利用AB垂直于x轴 得出 A（x，3log_ax），则正方形ABCD 的边长从横纵两个角度表示为log_ax=x²-x=2，求出x，再求a 即可．．

解答 解：设B（x，2log_ax），∵BC平行于x轴，∴C（x′，2log_ax）即log_ax′=2log_ax，∴x′=x²，
∴正方形ABCD边长=|BC|=x²-x=2，解得x=2．
由已知，AB垂直于x轴，∴A（x，3log_ax），正方形ABCD边长=|AB|=3log_ax-2log_ax=log_ax=2，即log_a2=2，∴a=$\sqrt{2}$，
故答案为：$\sqrt{2}$．

点评 本题考查对数函数的性质、对数的运算，是平面几何与函数知识的结合，体现出了数形结合的思想．