题目内容
已知函数f(x)=
,则f(f(
))= .
|
| π |
| 4 |
考点:三角函数的化简求值
专题:三角函数的求值
分析:依题意,可求得f(
)=-1,继而可得f(-1)的值.
| π |
| 4 |
解答:
解:∵f(
)=-tan
=-1,
∴f(f(
))=f(-1)=log2[(-1)2+3]=log24=2.
故答案为:2.
| π |
| 4 |
| π |
| 4 |
∴f(f(
| π |
| 4 |
故答案为:2.
点评:本题考查三角函数的化简求值,着重考查分段函数的应用,求值时由内向外是关键,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知函数f(x)=
,则不等式f(x)>0的解集为( )
|
| A、.{x|0<x<1} |
| B、{x|-1<x≤0} |
| C、{x|x>-1} |
| D、{x|-1<x<1} |
在△ABC中,角A,B,C所对的边分别为a,b,c,若a=1,b=
,A=30° 则角B等于( )
| 3 |
| A、60°或120° |
| B、30°或150° |
| C、60° |
| D、120° |
下列函数中,与函数y=x相同的函数是( )
A、y=
| ||||
B、y=(
| ||||
| C、y=lg10x | ||||
| D、y=2log2x |
过点P(-4,1)且与直线3x-4y+6=0垂直的直线方程是( )
| A、4x-3y-19=0 |
| B、4x+3y+13=0 |
| C、3x-4y-16=0 |
| D、3x+4y-8=0 |
已知向量
=(1,-2),
=(-
,y),若
∥
,则y=( )
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、1 | B、-1 | C、2 | D、-2 |
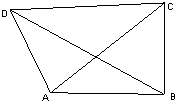 如图:在平面四边形ABCD中,AB=3
如图:在平面四边形ABCD中,AB=3