题目内容
已知向量
=（1，-2），
=（-
，y），若
∥
，则y=（ ）
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| A、1 | B、-1 | C、2 | D、-2 |
考点：平面向量共线（平行）的坐标表示
专题：平面向量及应用
分析：直接利用向量的共线的充要条件列出方程求解即可．
解答：
解：向量
=（1，-2），
=（-
，y），若
∥
，
所以-2×(-
)=y，解得y=1．
故选：A．
| a |
| b |
| 1 |
| 2 |
| a |
| b |
所以-2×(-
| 1 |
| 2 |
故选：A．
点评：本题考查向量的共线条件的应用，基本知识的考查．
练习册系列答案
相关题目
函数f(x)=
的定义域是（ ）
| 1 |
| log3(x-2) |
| A、（-∞，2） |
| B、（2，+∞） |
| C、（2，3）∪（3，+∞） |
| D、（2，5）∪（5，+∞） |
设集合A={x|y=
}，B={y|y=2x，x＞1}，则A∩B为（ ）
| 3x-x2 |
| A、[0，3] |
| B、（2，3] |
| C、[3，+∞） |
| D、[1，3] |
要得到函数y=cos(2x-
)的图象，可由函数y=cos2x的图象（ ）
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
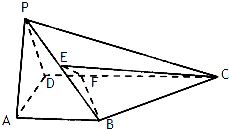如图，在四棱锥P-ABCD中，AB⊥平面PAD，AB∥CD，△PAD是边长为