题目内容

椭圆
x2
3
+
y2
2
=1的左右焦点分别为F1和F2，直线l1过F2且与x轴垂直，动直线l2与y轴垂直，l2交l1于点P，求线段P F1的垂直平分线与 l2的交点M的轨迹方程，并说明曲线类型．
考点：圆锥曲线的轨迹问题
专题：圆锥曲线的定义、性质与方程
分析：由题意可知：点M到定直线l1与到定点F1的距离相等，因此其轨迹是抛物线，点F1（-1，0）为焦点，直线l1为准线．
解答： 解：如图所示，
由题意可知：点M到定直线l1与到定点F1的距离相等，因此其轨迹是抛物线，点F1（-1，0）为焦点，直线l1为准线．
∴点M的轨迹为y2=-4x．
点评：本题考查了抛物线的定义、线段垂直平分线的性质，考查了推理能力，属于中档题．
练习册系列答案
相关题目
化简：
（1）sin（180°+α）+cos（270°+α）；
（2）
sin(π+α)tan(π-α)
sin(2π+α)tan(2π+α)
．
设Sn=
1
1×2
+
1
2×3
+
1
3×4
+…+
1
n(n+1)
，写出S1，S2，S3，S4的归纳并猜想出结果，并给出证明．
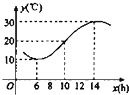某地一填从6时至14时的温度函数变化曲线近似满足y=Asin（ωx+φ）+b（|φ|＜π）
（1）求这段时间的最高和最低气温；
（2）求A，ω，φ，b的值．
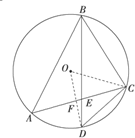如图，⊙O是△ABC的外接圆，D是 
AC
的中点，BD交AC于E．
（1）若CD=2
3
，O到AC的距离为1，求⊙O的半径r；
（2）求证：DC2=DE•DB．
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系的x轴的正半轴重合，且两个坐标系的坐标长度相同，已知直线l的参数方程为
x=-1+tcosα
y=1+tsinα
（t为参数），曲线C的极坐标方程为ρ=4cosθ．
（1）若直线l的斜率为-1，求直线l与曲线C交点的极坐标；
（2）若直线l与曲线C相交弦长为2
3
，求直线l的参数方程．
画出函数f（x）=loga 
1
x
 （a＞1 ）的大致图象．
函数f（x）=
a
x
+lnx-1（a是常数），
（1）讨论f（x）的单调区间；
（2）当a=1时，方程f（x）=m在x∈[
1
e
，e]上有两解，求m的取值范围；（e≈2.71828）
若两个等差数列{an}、{bn}的前Sn项和分别为Sn、Tn，对任意的n∈N*都有
Sn
Tn
=
2n-1
4n-3
，则
a5
b5
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网