题目内容
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合,且两个坐标系的坐标长度相同,已知直线l的参数方程为
(t为参数),曲线C的极坐标方程为ρ=4cosθ.
(1)若直线l的斜率为-1,求直线l与曲线C交点的极坐标;
(2)若直线l与曲线C相交弦长为2
,求直线l的参数方程.
|
(1)若直线l的斜率为-1,求直线l与曲线C交点的极坐标;
(2)若直线l与曲线C相交弦长为2
| 3 |
考点:参数方程化成普通方程
专题:直线与圆,坐标系和参数方程
分析:本题(1)将曲线C的极坐标方程化成直角坐标方程,将直线l的参数方程化成普通方程,求出它们交点的直角坐标,再化成极坐标;(2)利用直线与圆相交的弦长与弦心距的关系,求出直线的斜率,得到直线的普通方程,再将普通方程化成参数方程.
解答:
解:(1)∵直线l的参数方程为
(t为参数),直线l的斜率为-1,
∴直线l的普通方程为y-1=-(x+1)即y=-x.
∵曲线C的极坐标方程为ρ=4cosθ,
∴ρ2=4ρcosθ,
∵
,
∴x2+y2-4x=0.
由
得:2x2-4x=0,
∴直线l与曲线C交点的三角坐标为A(0,0),B(2,-2).
由
,
得直线l与曲线C交点的极坐标为A(0,0),B(2
,
π).
(2)∵直线l的参数方程为
(t为参数),
∴直线l过定点(-1,1),
设直线l的方程为y-1=k(x+1),(k存在)
即kx-y+k+1=0.
圆心C到直线l的距离为d=
=
.
∵直线l与曲线C相交弦长为2
,
∴r2-d2=(
)2,
∴
=1,
∴k=0或k=-
.
∴直线l的参数方程为
或
(t为参数).
|
∴直线l的普通方程为y-1=-(x+1)即y=-x.
∵曲线C的极坐标方程为ρ=4cosθ,
∴ρ2=4ρcosθ,
∵
|
∴x2+y2-4x=0.
由
|
得:2x2-4x=0,
∴直线l与曲线C交点的三角坐标为A(0,0),B(2,-2).
由
|
得直线l与曲线C交点的极坐标为A(0,0),B(2
| 2 |
| 7 |
| 4 |
(2)∵直线l的参数方程为
|
∴直线l过定点(-1,1),
设直线l的方程为y-1=k(x+1),(k存在)
即kx-y+k+1=0.
圆心C到直线l的距离为d=
| |2k-0+k+1| | ||
|
| |3k+1| | ||
|
∵直线l与曲线C相交弦长为2
| 3 |
∴r2-d2=(
| 3 |
∴
| |3k+1| | ||
|
∴k=0或k=-
| 3 |
| 4 |
∴直线l的参数方程为
|
|
点评:本题考查了极坐标与直角坐标的关系,参数方程与普通方程的关系,以及圆中弦长与弦心距的关系,本题思维量不大,但计算量较大,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

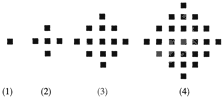 某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.