题目内容
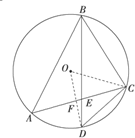如图，⊙O是△ABC的外接圆，D是  |
| AC |
（1）若CD=2
| 3 |
（2）求证：DC2=DE•DB．
考点：相似三角形的判定
专题：立体几何
分析：（1）OD⊥AC，设垂足为F，求出CF2=r2-1，利用DC2=CF2+DF2，建立方程，即可求得⊙O的半径．
（2）先证明△BCD∽△CED，可得
=
，从而问题得证；
（2）先证明△BCD∽△CED，可得
| DE |
| DC |
| DC |
| DB |
解答：
解：（1）∵D是
的中点，∴OD⊥AC，
设OD与AC交于点F，则OF=1，
在Rt△COF中，OC2=CF2+OF2，即CF2=r2-1，
在Rt△CFD中，DC2=CF2+DF2，
∴（2
）2=r2-1+（r-1）2，
解得r=3．
证明：（2）由D为
中点知，∠ABD=∠CBD，
又∵∠ABD=∠ECD，
∴∠CBD=∠ECD，
又∠CDB=∠EDC，
∴△BCD～△CED，
∴
=
，
∴DC2=DE•DB；
|
| AC |
设OD与AC交于点F，则OF=1，
在Rt△COF中，OC2=CF2+OF2，即CF2=r2-1，
在Rt△CFD中，DC2=CF2+DF2，
∴（2
| 3 |
解得r=3．
证明：（2）由D为
| AC |
又∵∠ABD=∠ECD，
∴∠CBD=∠ECD，
又∠CDB=∠EDC，
∴△BCD～△CED，
∴
| DE |
| DC |
| DC |
| DB |
∴DC2=DE•DB；
点评：本题是选考题，考查几何证明选讲，考查三角形的相似与圆的性质，属于基础题．
练习册系列答案
相关题目
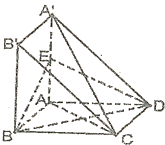如图，四边形ABCD与A′ABB′都是边长为a的正方形，点E是A′A的中点，AA′⊥平面ABCD