Question

已知椭圆Γ：

x2

4

+y2=1．
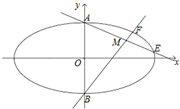
（1）椭圆Γ的短轴端点分别为A，B（如图），直线AM，BM分别与椭圆Γ交于E，F两点，其中点M（m，

1

2

）满足m≠0，且m≠±

3

．
①证明直线EF与y轴交点的位置与m无关；
②若△BME面积是△AMF面积的5倍，求m的值；
（2）若圆φ：x²+y²=4．l₁，l₂是过点P（0，-1）的两条互相垂直的直线，其中l₁交圆φ于T、
R两点，l₂交椭圆Γ于另一点Q．求△TRQ面积取最大值时直线l₁的方程．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题

分析：（1）①设出AM和BM的方程，与椭圆方程联立表示出E，F的坐标，用两点式写出EF的方程，令x=0即可确定与y轴的交点；
②根据△BME面积是△AMF面积的5倍可推出5|MA||MF|=|MB||ME|，从而建立关于m的方程，求解即可；
（2）直接设出两条直线方程，联立直线与圆的方程，利用根与系数的关系，表示出|OP|，然后表示出△TRQ面积，利用基本不等式可求出最大值，并确定直线方程．

解答： 解：（1）①A（0，1），B（0，-1），M （m，

1

2

），且m≠0，
∴直线AM的斜率为k1=-

1

2m

，直线BM斜率为k2=

3

2m

，
∴直线AM的方程为y=-

1

2m

x+1，
直线BM的方程为y=

3

2m

x-1．
由

x2 4 +y2=1 y=- 1 2m x+1

得（m²+1）x²-4mx=0，
∴x=0或x=

4m

m2+1

．
∴E点的坐标为（

4m

m2+1

，

m2-1

m2+1

）．
由

x2 4 +y2=1 y= 3 2m x-1

得（m²+9）x²-12mx=0，
解得x=0或x=

12m

m2+9

．
∴F点的坐标为（

12m

m2+9

，

9-m2

m2+9

）；                                
由已知，m≠0，m²≠3，
∴直线EF的斜率
k=

m2-1 1+m2 - 9-m2 9+m2

4m 1+m2 - 12m 9+m2

=

(m2+3)(m2-3)

-4m(m2-3)

=-

m2+3

4m

．
∴直线EF的方程为 y-

m2-1

m2+1

=-

m2+3

4m

(x-

4m

m2+1

)，
令x=0，得y=2，
∴EF与y轴交点的位置与m无关．
②S△AMF=

1

2

|MA||MF|sin∠AMF，S△BME=

1

2

|MB||ME|sin∠BME，
∠AMF=∠BME，5S_△AMF=S_△BME，
∴5|MA||MF|=|MB||ME|，
∴

5|MA|

|ME|

=

|MB|

|MF|

，
∴

5m

4m m2+1 -m

=

m

12m 9+m2 -m

，（m≠0），
∴整理方程得

1

m2+1

=

15

m2+9

-1，
即（m²-3）（m²-1）=0，
又∵m≠±

3

，
∴m²-3≠0，
∴m²=1，
∴m=±1
（2）∵直线l₁⊥l₂，且都过点P（0，-1），
∴设直线l₁：y=kx-1，
即kx-y-1=0．
直线l2：y=-

1

k

x-1，
即x+ky+k=0，
∴圆心（0，0）到直线l₁的距离为d=

1

1+k2

，
∴直线l₁被圆x²+y²=4所截的弦
|TR|=2

4-d2

=

2 3+4k2

1+k2

；
由

x+ky+k=0 x2 4 +y2=1

得，
k²x²+4x²+8kx=0，
∴xQ+xP=-

8k

k2+4

，
∴|QP|=

(1+ 1 k2 )• 64k2 (k2+4)2

=

8 k2+1

k2+4

．
∴S△TRQ=

1

2

|QP|•|TR|=

8 k2+1

k2+4

=

32

4k2+3 + 13 4k2+3

≤

32

2 13

=

16 13

13

．
当

4k2+3

=

13

4k2+3

，
即k=±

10

2

时等号成立，
此时直线l1：y=±

10

2

x-1

点评：本题考查直线与圆的位置关系，直线与椭圆的位置关系，基本不等式等知识的灵活应用，以及舍而不求的思想方法．属于难题．