题目内容
16.已知2cos2x+sin2x=Asin(ωx+φ)+b(A>0,0<φ<π),则A,φ,b的值分别为( )| A. | $A=2,φ=\frac{π}{4},b=1$ | B. | $A=\sqrt{2},φ=\frac{π}{6},b=2$ | C. | $A=\sqrt{2},φ=\frac{π}{6},b=1$ | D. | $A=\sqrt{2},φ=\frac{π}{4},b=1$ |
分析 利用三角恒等变换化简等式的坐标,从而比较系数求得A,φ,b的值.
解答 解:∵2cos2x+sin2x=Asin(ωx+φ)+b(A>0,0<φ<π),∴cos2x+sin2x+1=Asin(ωx+φ)+b,
即 $\sqrt{2}$sin(2x+$\frac{π}{4}$)+1=Asin(ωx+φ)+b,∴A=$\sqrt{2}$,ω=2,φ=$\frac{π}{4}$,b=1,
故选:A.
点评 本题主要考查三角恒等变换,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.近年来我国电子商务行业迎来篷勃发展的新机遇,2016年双11期间,某购物平台的销售业绩高达一千多亿人民币.与此同时,相关管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(Ⅰ)请完成如下列联表;
(Ⅱ)是否可以在犯错误的概率不超过0.1%的前提下,认为商品好评与服务好评有关?
(Ⅲ)若针对商品的好评率,采用分层抽样的方式从这200次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.
${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
(Ⅰ)请完成如下列联表;
| 对服务好评 | 对服务不满意 | 合计 | |
| 对 商品 好评 | |||
| 对商品不满意 | |||
| 合 计 |
(Ⅲ)若针对商品的好评率,采用分层抽样的方式从这200次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
8.下列函数在(0,+∞)上是减函数的是( )
| A. | f(x)=lnx | B. | f(x)=e-x | C. | $f(x)=\sqrt{x}$ | D. | $f(x)=-\frac{1}{x}$ |
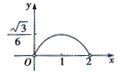
 如图,在侧棱长和底面边长均为2的正三棱柱ABC-A1B1C1中,点M、N、P分别在AA1、BC、BB1上运动,且AM=CN=B1P=X(0<X<2).记三棱锥P-MNB1的体积为,V(X)则函数Y=V(X)的图象大致为( )
如图,在侧棱长和底面边长均为2的正三棱柱ABC-A1B1C1中,点M、N、P分别在AA1、BC、BB1上运动,且AM=CN=B1P=X(0<X<2).记三棱锥P-MNB1的体积为,V(X)则函数Y=V(X)的图象大致为( )



 如图都是边长为1的正方体叠成的几何体,例如第(1)个几何体的表面积为6个平方单位,第(2)个几何体的表面积为18个平方单位,第(3)个几何体的表面积是36个平方单位.依此规律,则第n个几何体的表面积是3n(n+1)个平方单位.
如图都是边长为1的正方体叠成的几何体,例如第(1)个几何体的表面积为6个平方单位,第(2)个几何体的表面积为18个平方单位,第(3)个几何体的表面积是36个平方单位.依此规律,则第n个几何体的表面积是3n(n+1)个平方单位.