题目内容
4．
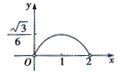如图，在侧棱长和底面边长均为2的正三棱柱ABC-A1B1C1中，点M、N、P分别在AA1、BC、BB1上运动，且AM=CN=B1P=X（0＜X＜2）．记三棱锥P-MNB1的体积为，V（X）则函数Y=V（X）的图象大致为（ ）| A． |  | B． |  | C． |  | D． |  |
分析 利用体积公式得出V（x）的解析式，从而可得出函数图象．
解答 解：M到平面BCC1B1的距离为d=$\sqrt{3}$，
S${\;}_{△{B}_{1}PC}$=$\frac{1}{2}×{B}_{1}P×BN$=$\frac{1}{2}$x（2-x），
∴V（x）=$\frac{1}{3}×\frac{1}{2}x（2-x）×\sqrt{3}$=$\frac{\sqrt{3}}{6}$x（2-x）．
∴V（x）的图象为开口向下的抛物线，对称轴为x=1．
故选C．
点评 本题考查了棱锥的体积公式，函数图象判断，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
12．为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列表：
（1）用分层抽样的方法在喜欢打蓝球的学生中抽6人，其中男生抽多少人？
（2）在上述抽取的6人中选2人，求恰有一名女生的概率．
（3）为了研究喜欢打蓝球是否与性别有关，计算出K2，你有多大的把握认为是否喜欢打蓝球与性别有关？
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
下面的临界值表供参考：
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
（2）在上述抽取的6人中选2人，求恰有一名女生的概率．
（3）为了研究喜欢打蓝球是否与性别有关，计算出K2，你有多大的把握认为是否喜欢打蓝球与性别有关？
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
下面的临界值表供参考：
| p（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9．已知x，y取值如表，画散点图分析可知y与x线性相关，且求得回归方程为$\widehaty=3x-5$，则m的值为3．
| x | 0 | 1 | 3 | 5 | 6 |
| y | 1 | 2m | 3-m | 3.8 | 9.2 |
16．已知2cos2x+sin2x=Asin（ωx+φ）+b（A＞0，0＜φ＜π），则A，φ，b的值分别为（ ）
| A． | $A=2，φ=\frac{π}{4}，b=1$ | B． | $A=\sqrt{2}，φ=\frac{π}{6}，b=2$ | C． | $A=\sqrt{2}，φ=\frac{π}{6}，b=1$ | D． | $A=\sqrt{2}，φ=\frac{π}{4}，b=1$ |
20．
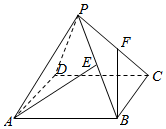已知正四棱锥P-ABCD中，PA=AB=2，E，F分别是PB，PC的中点，则异面直线AE与BF所成角的余弦值为（ ）
已知正四棱锥P-ABCD中，PA=AB=2，E，F分别是PB，PC的中点，则异面直线AE与BF所成角的余弦值为（ ）| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{6}}}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{2}$ |