题目内容
12．
如图都是边长为1的正方体叠成的几何体，例如第（1）个几何体的表面积为6个平方单位，第（2）个几何体的表面积为18个平方单位，第（3）个几何体的表面积是36个平方单位．依此规律，则第n个几何体的表面积是3n（n+1）个平方单位．
分析 结合图形，发现第（1）个图形的表面积是1×6=6，第（2）个图形的表面积是（1+2）×6=18，第（3）图形的表面积是（1+2+3）×6=36；以此类推即可求解．
解答 解：结合图形，发现：
第（1）个图形的表面积是1×6=6，
第（2）个图形的表面积是（1+2）×6=18，
第（3）图形的表面积是（1+2+3）×6=36，
第（4）图形的表面积是（1+2+3+4）×6=60，
…
故第n个图形的表面积是（1+2+3+…+n）×6=3n（n+1）
故答案为：3n（n+1）
点评 本题考查的知识点是归纳推理，其中从已知中的四个图形中，找出其表面积的变化规律，并进行大胆推断，是解答本题的关键．
练习册系列答案
相关题目
16．已知2cos2x+sin2x=Asin（ωx+φ）+b（A＞0，0＜φ＜π），则A，φ，b的值分别为（ ）
| A． | $A=2，φ=\frac{π}{4}，b=1$ | B． | $A=\sqrt{2}，φ=\frac{π}{6}，b=2$ | C． | $A=\sqrt{2}，φ=\frac{π}{6}，b=1$ | D． | $A=\sqrt{2}，φ=\frac{π}{4}，b=1$ |
如图是某社区的部分规划设计图，住宅区一边的边界曲线记为C，步行街（宽度不计）所在直线L与曲线C相切于点M，以点E为圆心，1百米为半径的圆的四分之一为大型超市，为方便住宅区居民购物休闲，该社区计划在步行街与大型超市之间铺设一条连接道路AB（宽度不计）以及修建花园广场．
20．
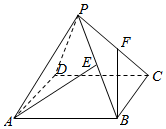已知正四棱锥P-ABCD中，PA=AB=2，E，F分别是PB，PC的中点，则异面直线AE与BF所成角的余弦值为（ ）
已知正四棱锥P-ABCD中，PA=AB=2，E，F分别是PB，PC的中点，则异面直线AE与BF所成角的余弦值为（ ）| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{6}}}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{2}$ |
1．在正四面体P-ABC体积为V，现内部取一点S，则$\frac{V}{3}＜{V_{S-ABC}}＜\frac{V}{2}$的概率为（ ）
| A． | $\frac{37}{216}$ | B． | $\frac{8}{27}$ | C． | $\frac{91}{216}$ | D． | $\frac{13}{27}$ |