题目内容
抛物线C的顶点在坐标原点，对称轴为y轴，若过点M（0，1）任作一直线交抛物线C于A（x1，y1），B（x2，y2）两点，且x1•x2=-4，则抛物线C的方程为 ．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：考虑本题是填空题，可一般问题特殊化，根据题意可设抛物线的方程为x2=2py（p＞0），过点M（0，1）任作一条直线交抛物线C于A（x1，y1），B（x2，y2）两点都有x1•x2=-4，特殊情况也成立，故考虑直线为y=1时，分别求出A、B的坐标，从而可求抛物线C的方程．
解答：
解：（一般问题特殊化）根据题意可设抛物线的方程为x2=2py（p＞0）
过点M（0，1）任作一条直线交抛物线C于A（x1，y1），B（x2，y2）两点都有x1•x2=-4，
考虑特殊情况也成立，故考虑直线为y=1时，可得A（-
，1），B（
，1），
则有x1x2=-2p=-4，∴p=2
故答案为：x2=4y．
过点M（0，1）任作一条直线交抛物线C于A（x1，y1），B（x2，y2）两点都有x1•x2=-4，
考虑特殊情况也成立，故考虑直线为y=1时，可得A（-
| 2p |
| 2p |
则有x1x2=-2p=-4，∴p=2
故答案为：x2=4y．
点评：本题主要考查了抛物线方程的求解，要注意解答本题时应用到的方法：一般问题特殊化可以减少运算．
练习册系列答案
相关题目
设集合A={x|x2-3x+4≥0}，集合B={x|log2x＞1}，则A∩∁RB=（ ）
| A、（-∞，2） |
| B、（-∞，2] |
| C、（0，2） |
| D、（0，2] |
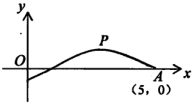如图，是函数y=Asin（ωx+φ）（A＞0，ω＞0，-π＜φ＜π）的图象的一段，O坐标原点，P（3，1）是该段图象的最高点，A（5，0）是该段图象与x轴的一个交点，则此函数的解析式为