题目内容
设集合A={x|x2-3x+4≥0}，集合B={x|log2x＞1}，则A∩∁RB=（ ）
| A、（-∞，2） |
| B、（-∞，2] |
| C、（0，2） |
| D、（0，2] |
考点：交、并、补集的混合运算
专题：集合
分析：分别求出A与B中不等式的解集确定出A与B，求出B的补集，找出A与B补集的交集即可．
解答：
解：由A中的不等式x2-3x+4≥0，得到△=9-16=-7＜0，
∴此不等式解集为R，即A=R，
由B中的不等式变形得：log2x＞1=log22，
解得：x＞2，
∴B=（2，+∞），
∵全集为R，∴∁RB=（-∞，2]，
则A∩（∁RB）=（-∞，2]．
故选：B．
∴此不等式解集为R，即A=R，
由B中的不等式变形得：log2x＞1=log22，
解得：x＞2，
∴B=（2，+∞），
∵全集为R，∴∁RB=（-∞，2]，
则A∩（∁RB）=（-∞，2]．
故选：B．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
相关题目
如图，在半径为R的圆C中，已知弦AB的长为5，则
•
=（ ）
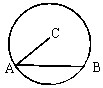
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法错误的是（ ）
| A、用平行于棱锥底面的平面去截棱锥，底面与截面之间的部分，这样的多面体叫做棱台 |
| B、有两个面平行，其余各个面都是梯形的几何体一定都是棱台 |
| C、圆锥的轴截面是等腰三角形 |
| D、用一个平面去截球，截面是圆 |