题目内容
对具有线性相关关系的变量x,y,测得一组数据如下表:
参考公式:b=
根据上表,利用最小二乘法得它们的回归直线方程为
=bx+1.5,据此模型来预测当x=20时,y的估计值为( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
| |||||||
|
| ∧ |
| y |
| A、210.5 | B、212.5 |
| C、210 | D、211.5 |
考点:线性回归方程
专题:计算题,概率与统计
分析:求出横标和纵标的平均数,写出样本中心点,把样本中心点代入线性回归方程,得到关于b的方程,解方程求出b,最后将x=20代入求出相应的y即可.
解答:
解:∵
=
=5,
=
=54
∴这组数据的样本中心点是(5,54)
把样本中心点代入回归直线方程
=bx+1.5,∴54=5b+1.5,
∴b=10.5,
∴回归直线方程为
=10.5x+1.5,
当x=20时,
=10.5×20+1.5=211.5,
故选:D.
. |
| x |
| 2+4+5+6+8 |
| 5 |
. |
| y |
| 20+40+60+70+80 |
| 5 |
∴这组数据的样本中心点是(5,54)
把样本中心点代入回归直线方程
| ∧ |
| y |
∴b=10.5,
∴回归直线方程为
| ∧ |
| y |
当x=20时,
| ∧ |
| y |
故选:D.
点评:本题考查线性回归方程,解题的关键是线性回归直线一定过样本中心点,这是求解线性回归方程的步骤之一.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,角A、B、C的对边分别是a、b、c.若asinA+csinC-
asinC=bsinB.则角B等于( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设α、β是两个不重合的平面,m、n是两条不重合的直线,则以下结论错误的是( )
| A、若α∥β,m?α,则 m∥β |
| B、若m∥α,m∥β,α∩β=n,则 m∥n |
| C、若m?α,n?α,m∥β,n∥β,则α∥β |
| D、若m∥α,m⊥β,则α⊥β |
设复数z=
,则复数z2的实部与虚部的和为( )
| 2i |
| -1+i |
| A、0 | B、2 | C、-2 | D、4 |
已知变量x,y满足约束条件
,若x+2y≥-5恒成立,则实数a的取值范围为( )
|
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、[-1,1] |
| D、[-1,1) |

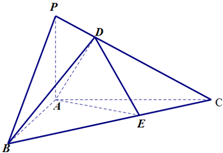 如图,在△ABC中,∠BAC=90°,AC=2AB,PA垂直△ABC所在的平面,PC与△ABC所在的平面成30°角,点D在线段PC上,点E在线段BC上.
如图,在△ABC中,∠BAC=90°,AC=2AB,PA垂直△ABC所在的平面,PC与△ABC所在的平面成30°角,点D在线段PC上,点E在线段BC上.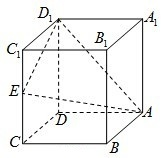 如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )
如图,在正方体ABCD-A1B1C1D1中,E是棱CC1的中点,F是侧面B1BCC1上的动点,并且A1F∥平面AED1,则动点F的轨迹是( )